Click to
view article in PDF format.
Click to
view article in PDF format.
GCMapping Geologic Features Using Seismic Curvature*
By
Satinder Chopra1 and Kurt J. Marfurt2
Search and Discovery Article #40272 (2008)
Posted February 7, 2008
*Adapted from the Geophysical Corner column, prepared by the authors, in AAPG Explorer, November, 2007, Part 1, entitled “Using Curvature to Map Faults, Fractures”, and December, 2007, Part 2, entitled “Curvature Can Be a Map to Clarity”. Editor of Geophysical Corner is Bob A. Hardage ([email protected]). Managing Editor of AAPG Explorer is Vern Stefanic; Larry Nation is Communications Director.
1Arcis Corporation, Calgary, Canada ([email protected])
2University of Oklahoma ([email protected])
General Statement
Curvature is a measure of the deviation of a surface from a plane. The more a surface is structurally flexed, folded or faulted, the larger its curvature. Curvature can indicate domes and sags associated with salt and shale diapirism, differential compaction, and diagenetic dissolution and collapse, as well as predict paleostress and areas favorable for natural fractures.
Curvature is usually computed from picked horizon surfaces interpreted on 3-D seismic data volumes. An interpreter defines surface patches of a given size, which appropriate software algorithms then fit with a mathematical quadratic surface. Curvature measures computed from the coefficients of this quadratic surface include:
1) Curvedness.
2) Azimuth of minimum curvature.
3) Shape index.
4) Minimum, maximum, most-positive, most-negative.
5) Dip.
6) Strike curvatures.
We find the most-positive and most-negative curvatures to be the easiest measure to visually correlate to features of geologic interest.
|
uFigure CaptionsuMethoduFaults and Fractures
uFigure CaptionsuMethoduFaults and Fractures
uFigure CaptionsuMethoduFaults and Fractures
uFigure CaptionsuMethoduFaults and Fractures
uFigure CaptionsuMethoduFaults and Fractures
uFigure CaptionsuMethoduFaults and Fractures
|
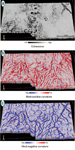
MethodFigure 1a shows a time-structure map at about 1850 ms, interpreted from a 3-D seismic volume acquired in Alberta, Canada. The horizon was manually picked across a grid of control lines to generate the horizon-based curvature images displayed in Figures 1b and 1c. Both of these displays are contaminated by strong N-S and E-W acquisition footprints. Whether due to limitations in the survey design, coherent noise, or systematic errors in data processing, an acquisition footprint is related to the source and receiver geometry and has little correlation to the subsurface geology. Horizons picked on noisy seismic data contaminated with acquisition footprint, or picked through regions where no consistent impedance contrast exists (such as channels, turbidites, mass transport complexes, and karst), can lead to inferior curvature measures. A significant advance in curvature analysis has been the volumetric estimation of curvature, which alleviates the need for picking horizons in regions where no continuous surface exists. Even when spatial filtering is used to minimize effects of an acquisition footprint, horizon-based curvature estimates may still suffer from footprint artifacts. In contrast, curvature attribute values extracted from volumetric curvature computations yield displays that are free of artifacts and make more geologic sense.
Faults and FracturesAs examples, Figures 1d and 1e show the most-positive and most-negative volumetric curvature attributes extracted along the horizon surface in Figure 1a. Notice that these displays are free of the N-S and E-W artifacts seen in Figures 1b and 1c, and show arcuate folds indicated by yellow arrows. The advantages of volumetric attributes are two-fold: 1) As shown in Figure 1, the images have a higher signal-to-noise ratio. Volumetric estimates of curvature are computed not from one picked data sample, but rather from a vertical window of seismic samples (in our case, 11 samples) and are statistically less sensitive to noise. 2) Not every geologic feature that we wish to interpret falls along a horizon that can be interpreted. Often the target of interest falls above or below a strong, easily picked horizon.
Curvature images having different spatial wavelengths provide different perspectives of the same geology. Tight (short-wavelength) curvature delineates small details, such as intense, highly localized fracture systems. Broad (long-wavelength) curvature enhances smooth, subtle flexures that are difficult to see in conventional seismic data, but which are often correlated to fracture zones that are below seismic resolution and to collapse features and diagenetic alterations.Figure 2 shows displays of strat-cubes near 1620 ms from coherence, most-positive (both long-wavelength and short-wavelength) and from short-wavelength, most-negative curvature volumes that intersect a random line that cuts across the fault/fracture trends. The red peaks (Figures 2b and 2c) on the fault lineaments (running almost north-south) correlate with the upthrown signature on the seismic data. The most-negative curvature strat-slice (Figure 2d) shows the downthrown edges on both sides of the faults highlighted in blue. Figure 3a shows the horizon slice extracted from the most-positive curvature volume at a zone of interest. There are a number of fracture lineaments delineated by yellow picks. The density and orientations of these lineaments have been combined into the rose diagram shown in Figure 3b, which retains the colors of the lineaments. This rose diagram can be compared with a similar diagram obtained from borehole image logs to gain confidence in the seismic-to-log calibration. Once a favorable match is obtained, the interpretation of fault/fracture orientations and the intervals over which they dominate can then be trusted for a more quantitative analysis – which, in turn, is useful for optimal characterization of reservoirs.
Depositional FeaturesSo far we have demonstrated the application of the most-positive and most-negative curvature attributes for detecting faults and fractures and calibration with borehole image-log data. Now we illustrate the application of these attributes for mapping channels, levees and other stratigraphic features – particularly in older rocks that have undergone differential compaction. In Figure 4 we generate strat-cube displays through volumetric estimates of coherence, combined with most-positive and most-negative curvatures. A strat-cube is a sub-volume of seismic data or its attributes, either bounded by two horizons that may not necessarily be parallel, or spanning seismic data above and/or below a given horizon. The displayed surfaces are 4 ms below the horizon used for generating the strat-cube. Notice the clarity with which the north-south main channel stands out and a second channel in the top-right corner.Because of differential compaction and the presence of levees, the most-positive curvature defines the flanks of the channels, potential levees, and overbank deposits. The most-negative curvature highlights the channel axes or thalwegs. The coherence image is complementary and is insensitive to structural deformation of the surface; instead, it highlights those areas of the channel flanks where there is a lateral change in the waveform due to tuning.In Figure 5 we show a chair display for a strat-cube constructed from the most-positive curvature attribute volume and an associated seismic profile. Notice how the lineaments corresponding to the levees of the channels correlate with the localized “highs” on the seismic section. Once an interpreter is able to see such a convincing correlation, the interpretation of smaller lineaments can be performed with more confidence.
Diagenetic FeaturesIn Figure 6 we re-examine a survey discussed in detail by Sagan and Hart in the November, 2006, AAPG Bulletin on hydrothermally altered dolomite. In Figure 6a and 6b, respectively, we display time slices through the most-negative curvature volume at approximately the Trenton and basement levels. Note that by using a volumetric estimate of curvature, we can map the same diagenetically altered zones at the Trenton level and faults in the basement discussed by Sagan and Hart (2006). The structural control and diagenetic alteration result in a suite of en echelon valley-like features running northwest-southeast through the survey.
ConclusionsLike all attributes, curvature is valuable only when coupled with a geologic model of structural deformation, stratigraphic deposition, or diagenetic alteration. Curvature is particularly sensitive to flexures and faults. Curvature can be a powerful tool in mapping channels, levees, bars, contourites, and other stratigraphic features, particularly in older rocks that have undergone differential compaction. Discrete fractures often appear on most-negative curvature. This behavior can be caused by sags about the fractures or by local velocity changes associated with stress, porosity, diagenetic alteration, or fluid charge. Although curvature attributes calculated on time surfaces after spatial filtering can display interesting features, volumetric curvature attributes provide more valuable information on fracture orientation and density in zones where seismic horizons are not trackable.
Sagan, J.A., and B.S. Hart, 2006, Three-dimensional seismic-based definition of fault related porosity development: Trenton-Black River interval, Saybrook, Ohio: AAPG Bulletin, v. 90, p. 1763-1785.
The authors thank Arcis Corporation for permission to show the data examples and publish this work .
|