|
Figure Captions
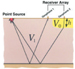 Figure 1.
Simple point-source/ receiver-array model with flat topography. The
static shift from Geophone 1 to Geophone 2 is Figure 1.
Simple point-source/ receiver-array model with flat topography. The
static shift from Geophone 1 to Geophone 2 is
Dtstatic=h[V1-V0]/V0V1
where
Dtstatic
is a first-order approximation assuming the angle from vertical of h is
small (ratio of V1/V0
is large).
 Figure 2. Static correction in ms/ft for
various surface alluvial velocities (V0)
and various underlying-layer velocities (V1).
The situation modeled, and equation used, is shown in Figure 1. The
static shifts for all V1
velocities above 8,000 ft/s are only slightly larger than for V1
= 8,000 ft/s. Figure 2. Static correction in ms/ft for
various surface alluvial velocities (V0)
and various underlying-layer velocities (V1).
The situation modeled, and equation used, is shown in Figure 1. The
static shifts for all V1
velocities above 8,000 ft/s are only slightly larger than for V1
= 8,000 ft/s.
 Figure 3. Four uninterpreted (top) and
interpreted (bottom) representative field files from a recent
ultra-shallow seismic-reflection survey near Great Bend, Kan. The
horizontal axis is source-to-receiver offset in feet. The source was a
single shot from a .22-caliber rifle, and the single-geophone group
interval is two inches. Digital frequency and f-k filtering has been
applied, as well as AGC scaling. The lateral distance from the shotpoint
on the left to the shotpoint on the right is 40 feet. Within that
distance, the weathering Figure 3. Four uninterpreted (top) and
interpreted (bottom) representative field files from a recent
ultra-shallow seismic-reflection survey near Great Bend, Kan. The
horizontal axis is source-to-receiver offset in feet. The source was a
single shot from a .22-caliber rifle, and the single-geophone group
interval is two inches. Digital frequency and f-k filtering has been
applied, as well as AGC scaling. The lateral distance from the shotpoint
on the left to the shotpoint on the right is 40 feet. Within that
distance, the weathering  velocity velocity changes from 518 ft/s to 682 ft/s,
without noticeable surface topographic or soil variation. The event in
blue is the water table, at a depth of eight feet. changes from 518 ft/s to 682 ft/s,
without noticeable surface topographic or soil variation. The event in
blue is the water table, at a depth of eight feet.
 Figure 4. Uninterpreted and interpreted field
file generated by stacking five spark-plug-generated events. Note the
time scale and that the near-source first-arrivals have a dominant
frequency greater than 1 kHz. Figure 4. Uninterpreted and interpreted field
file generated by stacking five spark-plug-generated events. Note the
time scale and that the near-source first-arrivals have a dominant
frequency greater than 1 kHz.
 Figure 5. A 1-D solution to the three-layer
problem from the first arrivals picked in Figure 4. Figure 5. A 1-D solution to the three-layer
problem from the first arrivals picked in Figure 4.
Static corrections are made to
seismic-reflection data to compensate for time shifts in the data caused
by changes in topography and variations in near-surface seismic-wave
 velocity velocity . Recent developments in ultra-shallow seismic imaging indicate
that static time shifts in seismic data caused by relatively small
changes in the thickness of very-low- . Recent developments in ultra-shallow seismic imaging indicate
that static time shifts in seismic data caused by relatively small
changes in the thickness of very-low- velocity velocity surficial layers may be
significant. surficial layers may be
significant.
The  velocity velocity -variation component of the
correction involves what is commonly called the "weathered zone." In
some places the weathered zone consists mostly of unconsolidated,
near-surface materials. It is not commonly realized that P-wave
velocities in these shallow, unconsolidated materials can be
substantially lower than the -variation component of the
correction involves what is commonly called the "weathered zone." In
some places the weathered zone consists mostly of unconsolidated,
near-surface materials. It is not commonly realized that P-wave
velocities in these shallow, unconsolidated materials can be
substantially lower than the  velocity velocity of sound in air. of sound in air.
The primary purpose of this article is to
show that when low- velocity velocity surface layers are present, a thickness of
even a few feet can have profound static effects. surface layers are present, a thickness of
even a few feet can have profound static effects.
Most methods used to attack the
static-correction problem depend upon using the near-surface  velocity velocity information obtainable from conventional seismic data. Methods include
refraction statics, surface-consistent statics, cross-correlation
statics and diving-wave tomography. In most commonly encountered
geologic situations one or more of the above-cited techniques may be
sufficient. When using source- and/or receiver arrays in which the
highest possible resolution is necessary, and under conditions where the
near- surface geological conditions change quickly and in unpredictable
ways, such approaches can be inadequate.
information obtainable from conventional seismic data. Methods include
refraction statics, surface-consistent statics, cross-correlation
statics and diving-wave tomography. In most commonly encountered
geologic situations one or more of the above-cited techniques may be
sufficient. When using source- and/or receiver arrays in which the
highest possible resolution is necessary, and under conditions where the
near- surface geological conditions change quickly and in unpredictable
ways, such approaches can be inadequate.
The problem in its most elementary form, with
a point source and a two-geophone receiver array, is depicted in Figure
1. Note that in this case the surface topography is flat, but there is a
variation in the thickness of the low- velocity velocity material (V0)
that overlies a higher- material (V0)
that overlies a higher- velocity velocity layer (V1).
When the layer (V1).
When the  velocity velocity of the near-surface material is substantially less
than the of the near-surface material is substantially less
than the  velocity velocity of a P-wave in air, only one or two feet of variation
in thickness in the near-surface layers can cause significant static
shifts. These problems can occur almost anywhere, but they are most
common where a variable thickness of alluvial, fluvial, aeolian or
glacial material overlies bedrock. of a P-wave in air, only one or two feet of variation
in thickness in the near-surface layers can cause significant static
shifts. These problems can occur almost anywhere, but they are most
common where a variable thickness of alluvial, fluvial, aeolian or
glacial material overlies bedrock.
The first-order static correction for the
geologic situation depicted in Figure 1 is shown graphically in
Figure 2: The amount of static correction necessary is highly dependent on the
 velocity velocity of the unconsolidated material (V0)
and is not strongly dependent on the of the unconsolidated material (V0)
and is not strongly dependent on the  velocity velocity of the underlying
higher- of the underlying
higher- velocity velocity layer (V1).
Under conditions similar to those presented in Figure
1, knowing both
the layer (V1).
Under conditions similar to those presented in Figure
1, knowing both
the  velocity velocity and the thickness of the V0
material is especially important. and the thickness of the V0
material is especially important.
Very-near-surface P-wave velocities are
commonly 800 to 1,500 ft/s. In Figure 2, the static correction for these
materials ranges from about 0.8 ms to 0.2 ms per foot of thickness,
respectively. The real problem arises when velocities of less than 600
ft/s are encountered in near-surface materials, as these low velocities
produce static corrections of more than 1 ms per foot of thickness. An
error of only one foot in calculating the thickness of near-surface
materials with a  velocity velocity of 500 ft/s, for example, results in a
static-correction error of 1.5 ms. of 500 ft/s, for example, results in a
static-correction error of 1.5 ms.
Many seismologists believe that P-wave
 velocity velocity in earth materials is never less than about 1,100 ft/s (the in earth materials is never less than about 1,100 ft/s (the
 velocity velocity of sound in air). The Wyllie-equation argument says that the
seismic P-wave of sound in air). The Wyllie-equation argument says that the
seismic P-wave  velocity velocity in a material is an average of the in a material is an average of the  velocity velocity in
the pore fluid (air) and the mineral grains through which the seismic
wave passes. This argument is used in the analysis of borehole sonic
logs in water-saturated solid rock, where it usually works quite well. in
the pore fluid (air) and the mineral grains through which the seismic
wave passes. This argument is used in the analysis of borehole sonic
logs in water-saturated solid rock, where it usually works quite well.
In reality, the Wyllie-equation argument has
very little to do with the P-wave  velocity velocity in unconsolidated materials
because in unconsolidated materials
because  velocity velocity is dependent only upon the shear modulus, the bulk
modulus, and the density of the total material, not on the average of
these properties for the constituent materials. The other reason that
1,100 ft/s is often quoted as a minimum is dependent only upon the shear modulus, the bulk
modulus, and the density of the total material, not on the average of
these properties for the constituent materials. The other reason that
1,100 ft/s is often quoted as a minimum  velocity velocity is that most seismic
sources emit some audible sound, called air wave, into the air. When the is that most seismic
sources emit some audible sound, called air wave, into the air. When the
 velocity velocity in the near- surface material is less than 1,100 ft/s, the
first arrival at geophones within a few feet of the shot is the air
wave. In such cases, investigators sometimes erroneously pick the air
wave as the first seismic P-wave arrival. in the near- surface material is less than 1,100 ft/s, the
first arrival at geophones within a few feet of the shot is the air
wave. In such cases, investigators sometimes erroneously pick the air
wave as the first seismic P-wave arrival.
Figure 3 shows four representative field
files from an ultra-shallow seismic-reflection survey conducted near the
Arkansas River a few miles east of Great Bend, Kan. The first
reflections come from the boundaries between intra-alluvial layers at
depths of two to four feet. The deepest reflection is from the water
table, at a depth of about eight feet. The interval  velocity velocity varies
quickly from less than 650 ft/s above the water table to more than 2,000
ft/s below it. varies
quickly from less than 650 ft/s above the water table to more than 2,000
ft/s below it.
To obtain this degree of detail, geophone
intervals of two inches were used. The seismic source was a single,
.22-caliber rifle shot, using short ammunition, with the tip of the
rifle barrel inserted about four inches into a 3/4-inch-diameter hole in
the ground. The dominant frequency is about 450 Hz, which, when combined
with the near-surface  velocity velocity of 623 ft/s, provides a 1/4-wave length
vertical resolution limit of approximately five inches. of 623 ft/s, provides a 1/4-wave length
vertical resolution limit of approximately five inches.
To determine the velocities even closer to
the surface, we have obtained P-wave  velocity velocity measurements with
refraction surveys using an automotive spark plug as an energy source.
We obtained a 100-foot-long spark-plug wire from an automotive supply
company and hooked one end of the wire to the distributor of a vehicle
and the other end to a spark plug placed in a hole 1/2-inch deep and
1/2-inch in diameter, located about one inch from the nearest geophone.
Although it has very low power, the spark plug is a highly-repeatable,
high-frequency source. measurements with
refraction surveys using an automotive spark plug as an energy source.
We obtained a 100-foot-long spark-plug wire from an automotive supply
company and hooked one end of the wire to the distributor of a vehicle
and the other end to a spark plug placed in a hole 1/2-inch deep and
1/2-inch in diameter, located about one inch from the nearest geophone.
Although it has very low power, the spark plug is a highly-repeatable,
high-frequency source.
Figure 4 shows a detailed ultra-shallow field
file from a test site in Lawrence, Kansas, using the spark-plug source.
The  velocity velocity of the near-surface material varies from about 450 ft/s to
about 1,000 ft/s (Figure 5). of the near-surface material varies from about 450 ft/s to
about 1,000 ft/s (Figure 5).
In the first section, we showed the potential
effects of very-low near-surface velocities on intra-array static
shifts. In the second section, we presented examples of seismic data in
which P-wave velocities as low as 450 ft/s were observed using both
reflection and refraction methods. Making static corrections becomes
more difficult as high-resolution seismic-reflection data are pushed to
progressively higher frequencies. For example, a static-correction error
of three ms would cause 160-Hz dominant-frequency seismic-reflection
data to stack 180 degrees out-of-phase. The static correction necessary
for varying thickness of low- velocity velocity unconsolidated materials is
sometimes in excess of one ms per foot of thickness of the material. unconsolidated materials is
sometimes in excess of one ms per foot of thickness of the material.
We believe that having accurate information about the  velocity velocity and
thickness of near-surface materials is essential to removing static
shifts in conventional reflection surveys when source- and/or receiver
arrays are used in a geologic region with very-low- and
thickness of near-surface materials is essential to removing static
shifts in conventional reflection surveys when source- and/or receiver
arrays are used in a geologic region with very-low- velocity velocity ,
near-surface materials. ,
near-surface materials.
Return
to top.
|
![]() Click to view this article in PDF format.
Click to view this article in PDF format.


 Figure 1.
Simple point-source/ receiver-array model with flat topography. The
static shift from Geophone 1 to Geophone 2 is
Figure 1.
Simple point-source/ receiver-array model with flat topography. The
static shift from Geophone 1 to Geophone 2 is Figure 2. Static correction in ms/ft for
various surface alluvial velocities (V
Figure 2. Static correction in ms/ft for
various surface alluvial velocities (V Figure 3. Four uninterpreted (top) and
interpreted (bottom) representative field files from a recent
ultra-shallow seismic-reflection survey near Great Bend, Kan. The
horizontal axis is source-to-receiver offset in feet. The source was a
single shot from a .22-caliber rifle, and the single-geophone group
interval is two inches. Digital frequency and f-k filtering has been
applied, as well as AGC scaling. The lateral distance from the shotpoint
on the left to the shotpoint on the right is 40 feet. Within that
distance, the weathering
Figure 3. Four uninterpreted (top) and
interpreted (bottom) representative field files from a recent
ultra-shallow seismic-reflection survey near Great Bend, Kan. The
horizontal axis is source-to-receiver offset in feet. The source was a
single shot from a .22-caliber rifle, and the single-geophone group
interval is two inches. Digital frequency and f-k filtering has been
applied, as well as AGC scaling. The lateral distance from the shotpoint
on the left to the shotpoint on the right is 40 feet. Within that
distance, the weathering  Figure 5. A 1-D solution to the three-layer
problem from the first arrivals picked in Figure 4.
Figure 5. A 1-D solution to the three-layer
problem from the first arrivals picked in Figure 4.