3-Dimensional Digital Outcrop Data Collection and Analysis Using Eye-safe Laser (LIDAR) Technology*
By
Jerome A. Bellian1, David C. Jennette1, Charles Kerans1, James Gibeaut1, John Andrews1, Brad Yssldyk2, David Larue3
Search and Discovery Article 40056 (2002)
*Adapted for online presentation from poster session at AAPG Convention, Houston, Texas, March 2002.
1The Bureau of Economic Geology, The University of Texas at Austin, TX ([email protected]; [email protected]; [email protected]) (www.beg.utexas.edu)
2Optech, Toronto, ON
3Chevron Petroleum Technology Company, San Ramon, CA ([email protected])
* Editorial Note: This article, which is highly graphic (or visual) in design, is presented as: (1) three posters, with (a) each represented in JPG by a small, low-resolution image map of the original; each illustration or section of text on each poster is accessible for viewing at screen scale (higher resolution) by locating the cursor over the part of interest before clicking; and (b) each represented by a PDF image, which contains the usual enlargement capabilities; and (2) searchable HTML text with figure captions linked to corresponding illustrations with descriptions.
Users without high-speed internet access to this article may experience significant delay in downloading some illustrations due to their sizes.
First Poster
Second Poster
Third Poster
Fourth Poster
Fifth Poster
Abstract
New efforts to integrate critical ground truthing from outcrop data into the rapidly evolving world of digital subsurface mapping and exploration have taken significant strides in the last decade. LIDAR (Light Detection And Ranging), a laser-based mapping tool developed for atmospheric studies in the mid-1960s, enables geologists to rapidly and accurately collect stratigraphic information directly from outcrops scanned with intensity-sensitive laser instrumentation. Light-ranging data is co-rendered with laser intensity data to generate 3D outcrop models with near zero distortion in x, y and z space. In addition, the intensity of the return signal helps to discriminate between different lithologic types. The results can be likened to black and white photography draped onto a 3D surface. Data acquisition can be done in any lighting conditions, with a rate of 2000 points per second.
This instrument can achieve sub-centimeter range resolution with 16-bit intensity returns for each ranging point recorded. A 1 x 0.3 km outcrop face can be acquired and merged into a single point-cloud dataset with corresponding intensity in less than two hours on a standard laptop computer. Case studies include deepwater carbonate and siliciclastic outcrops from West Texas and deepwater channel sandstones from northern Spain. These data are ideal for display and interpretation on workstation systems. Results are then directly imported into subsurface modeling software to measure and collect fine-scale bed-length data and to construct remarkably accurate architecture and lithofacies models.
|
|
Figure Captions (Concept, Workflow, and Model; Figures 1-1 to 1-7)
3D Outcrop to 3D Model Concept and Workflow
· Interpretation: Add stratigraphic interpretation to 3D photo-draped outcrop model.
The workflow for generating a photo-draped 3D outcrop model used as a foundation for complex geological models (Figure 1-1) begins with point cloud data and high-resolution photograph acquisition in the field. Once the data have been acquired, the individual datasets are merged into a unified coordinate system in InnovMetric's “Polyworks” software module “IMAlign.” After a single coordinate system has been defined for all datasets, the data can be filtered to generate a lower resolution TIN (triangulated irregular network) surface. The full-resolution intensity data are used to remove camera distortion from photos and both the photo and the intensity TIF image are applied as textures to the TIN terrain model. Finally, stratigraphic interpretations are then added.
LIDAR at The University of Texas at Austin
This thing called “LIDAR” is an acronym that describes a method of determining position of a target relative to some arbitrary reference point (Figure 1-2). LIDAR stands for Light Detection and Ranging. It was originally used by atmospheric and planetary geoscientists in the 1960s to image bodies of galactic matter and atmospheric plumes. LIDAR is Light Detection and Ranging; RADAR is Radio Detection and Ranging; SONAR is Sound Navigation and Ranging. LIDAR can be compared to other remote sensing techniques such as SONAR and RADAR, which also determine the position of distant targets from a known point.
The University of Texas at Austin is the only University in the world with Optech ALTM airborne and ILRIS 3D ground-based LIDAR instruments (Figures 1-3, 1-4, 1-5). The combination of these two instruments enables us to survey entire cities at up to millimeter point spacing in 3D.
Points and Intensity to Surface Model (Figure 1-6)
Point clouds are “smart-filtered” to eliminate excessive data overlap and normalize point distribution across the outcrop surface (1.), Figure 1-6). This step is extremely important to minimize file size and keep sufficient detail to accurately represent the true surface of the outcrop. The filtered x, y, and z data are then used to generate a TIN terrain model (2.), Figure 1-6).
A full-resolution intensity image is then matched to the terrain model. Since the intensity is from the x, y, and z laser return, it matches exactly to the TIN (3.), Figure 1-6). The result is a pseudo-black and white 3D photograph derived from laser-returned x, y, z and intensity data (4.), Figure 1-6). Multiple datasets can be merged into the same coordinate system in InnovMetric’s Polyworks CAD software without GPS coordinates as long as each image has sufficient overlap with the previous and next image (10% is more than enough). Stratigraphic interpretation can begin from this stage using the intensity data much as one would use a black and white outcrop photograph.
Digital Terrain Model-Photo Merge (Figure 1-7)
The process of adding a photograph to the x, y, z, and intensity model uses a “rubber-sheet” rectification technique (we used ER Mapper for this), where multiple control points are picked on each photo that correspond to points on an intensity image (Figure 1-7). Between 30 and 60 control points are used depending on the terrain complexity. Picking control points is fast and easy since the photo and the intensity image are acquired at the same time from the same vantage point. To generate a true 3D effect, we use angular variance normal to the dataset origin to define a best-fit image to color-map to the x, y, z pixels. For example, if the user wants to display all faces > 90 degrees from the normal to the TIN face with color pixels from image 1 and all faces from < 90 degrees with color pixels from image 2, this can be done using a “normal gate” as follows:
If (q>90) then C = Image1; if q<90 then C = Image2 Where q = viewers perspective angle with reference to face normal and C = color pixels to be mapped.
The technique allows us to map multiple images onto a single surface resulting in a full 3D textured surface. The textured surface is now optimized to any viewer perspective allowing the viewer to “see” around corners with full resolution. This technique also reduces “doubling up” of images from multiple perspectives and thereby reduces rendering time.
Figure Captions (Deep-Water Clastic Case Studies; Figures 2-1 to 3-8)
Deep-Water Clastic Case Studies
Ainsa, Northern Spain (Photo Drape)
The map view of the Ainsa 2 outcrop (Figure 2-1) shows the general outcrop trend were data were acquired. They were acquired with ILRIS 3D from the east side. For comparison, a standard 35 mm photo mosaic and a merged ILRIS 3D x, y, z, and intensity image looking from the same vantage point, are displayed together in Figure 2-2. Note the poor intensity returns from vegetation. These can be used to assist in the composition of vegetation removal algorithms.
The Ainsa deep-water sandstone outcrop from Northern Spain was selected to demonstrate the minimum level of resolution currently being achieved at the Jackson School of Geosciences at the University of Texas at Austin. The green pixels in the intensity images (Figure 2-3) are keyed to a linear cutoff of intensity values coded to display as green. Combining the image RGB and Intensity image improves the ability for us to remove vegetation without loosing valuable geological details. It also opens up the potential to use gated logic statements to filter out unwanted data or enhance desired data, like sand to shale ratios.
Intensity TIF + Original photo = Photo mapped onto intensity TIF Photo mapped onto intensity TIF
Photo mapped onto intensity TIF + X, Y, Z TIN = 3D photo draped model 3D photo draped model
Ainsa Quarry, Northern Spain (Variable Perspective)
The two images in Figure 2-5 illustrate perspective correction possibilities when using LIDAR. The photo mosaic (Figure 2-6) was taken from the same perspective as the ILRIS 3D data in Figure 2-6. The images in Figure 2-7 show the same outcrop as taken from an ultra-light aircraft and the same ILRIS 3D dataset tilted to adjust the perspective.
Brushy Canyon Formation, West Texas (Sand-Shale Discrimination)
Point clouds are assembled directly from individual x, y, z, and intensity data downloaded from ILRIS 3D (Figures 3-1, 3-2-3-3, 3-4). These data were acquired by the Bureau of Economic Geology and Optech in May, 2001, at an average spot spacing of 7 cm. The data acquisition of each of these datasets was approximately 15 minutes. These data are from a Permian deep-water, confined, channel complex (the “100 foot Channel” from former Exxon terminology) in Guadalupe Canyon, West Texas. In this example, the intensity values at each x, y, and z location are good sandstone-shale indicators. Simple intensity classification can yield instant net to gross relationships as well as vertical and horizontal sand bed continuity.
The scans in Figures 3-1, 3-2, 3-3, 3-4 are displayed in order to demonstrate that ILRIS 3D operates nearly identically to a conventional camera in so much as ILRIS 3D acquires image data in a direct line of sight. Therefore, data shadows may exist in areas where ILRIS cannot “see” from a single vantage point. In order to complete a full 3D model (eg. no data shadows), multiple datasets are required from multiple vantage points with some degree of overlap. ILRIS data may be processed with software that enables the user to pick one or several control points on various overlapping images to be merged (we use Polyworks by InnovMetrics). The data within the overlap-region are used to iterate to a minimum-3D-spatial error using hundreds of thousands of data points without the need for GPS (commonly iterate to 0.00000001 meters).
Solitary Channel, Southern Spain (3-Dimensionality Across Multiple Fault Blocks)
In Figure 3-5, each color indicates an individual dataset used to reconstruct the Solitary Channel, outcrop. For comparison, the same image displayed also in Figure 3-5 with intensity of each x, y, and z point in grayscale.
Figure 3-6 displays this tractional, conglomeratic channel fill by means of a photograph, an ILRIS 3D intensity image, and the same intensity image draped onto the TIN digital terrain model. The model enables the user to extract real dimensional data from the outcrop preserving spatial integrity of the deposit.
The Solitary Channel Outcrop in Southern Spain (Figures 3-5, 3-6, 3-7, 3-8) is an excellent mixed-conglomeratic/sandstone outcrop analogous to many clastic, West African, deep-water reservoirs. Understanding reservoir geometry and continuity at the sub-seismic scale can be accurately quantified through the use of dimensional data of well-exposed outcrops like this one. One the first questions the Solitary Channel outcrop presents us, however, is “What is horizontal?” With the aid of ILRIS 3D data, quantifying local and regional dip as well as steepness of channel incision can be accomplished. A second question is “How can we back out the post-depositional, structural modifications to this system to more fully understand the original bedding architecture?” Our ability to address questions like these quantitatively in the past required enormous investments in time and equipment to acquire even low resolution datasets. Merging the data into a single coordinate system required the use of GPS and the data processing time took months or even years before a usable geologic model could be achieved. Even then, most of the detail of the system was lost along the way. This entire outcrop was scanned at 10 cm or greater resolution (several 1 cm resolution windows were acquired for added detail in particularly difficult sections to correlate) in 2.5 days with two geologists. An additional 1 day with one geologist was required to merge all datasets (on a standard laptop in the field) into a single coordinate system exported and ready for stratigraphic interpretation.
Figure Captions (Carbonate Case Studies; Figures 4-1 to 4-6)
Carbonate Case Studies:Upper Hueco - Clear Fork Formations, West Texas: (Basin Geometry)
Shown on a digital elevation model of the Sierra Diablo Mountains (Figure 4-1) is the mouth of Victorio Canyon, where good outcrops of the Upper Hueco through Clear Fork Formations on both north- and south-facing canyon walls. The focus for this study is the area of north facing wall (blue box in Figure 4-2). It was scanned using Optech Laser Imaging’s ILRIS 3D ground-based LIDAR instrument in February, 2002 (Figure 4-3). The cross-section in Figure 4-4 illustrates slope and toe of slope deposits (late Wolfcampian through early Leonardian) Victorio Canyon, West Texas, that crop out along the north-facing wall of Victorio Canyon.
The images in Figure 4-5 illustrate both the photo pan and the ILRIS 3D LIDAR scan of the north facing wall of Victorio Canyon. The photo pan has stratigraphic interpretation in red, white and yellow whereas the ILIRS 3D point cloud does not. The transfer of these data from the photo pan onto the ILRIS 3D point cloud are currently in progress and are beginning to unravel new stratigraphic relationships previously undocumented with regard to three dimensionality of the exposure in Victorio Canyon. A complete model of the Sierra Diablo Mountains (Upper Hueco through Clear Fork Formations) is also in progress; the Victorio Canyon outcrop being the first of the batch.
The images in yellow and green boxes in Figure 4-6 are moderate resolution TIN and intensity images generated from the ILRIS point cloud data. The green coloration in these images is a linear, intensity cutoff indicating vegetation. Once photographs are applied to these data, red, green, blue, and intensity “attributes” can be used to aid in mapping various stratigraphic units. The yellow inset box shows the transition between TIN and point cloud and a close-up of the green “coded” vegetation. Return to top.
Figure Captions (Long-Range Goals, Looking Forward; Figures 5-1 to 5-5)
Long-Range Research Goals at the Bureau of Economic Geology
Ground based LIDAR (Figure 5-2) is a tool that provides geologists a quick, accurate, quantitative tool to better understand stratigraphic relationships at the sub-seismic scale. The use of an instrument that can easily lend high resolution photographic integration combines the old and the new as far as outcrop analysis goes. In order to build more accurate reservoir models, we need to acquire more accurate data from which to build reservoir models. LIDAR provides a safe, fast, effective, and inexpensive method of gathering enormous amounts of highly accurate data with a minimum of “down time” between acquisition and generation of a geological model.
Conclusions
Photo-pan geology has worked well for us in the past, much in the way that 2D seismic worked for us in the past and still has its place in our geological tool box. It seems clear, however, that, like the advent of 3D seismic, 3D outcrop photographic modeling is the next logical step to quantify what we see in order to better select analogs for what we cannot see in the subsurface. 3D imaging and digital outcrop analysis are becoming as critical as the Brunton compass and the hand lens. The more quantitative we can be in our understanding of depositional systems, the better we will become at predicting ahead of the bit with more unknowns due to fewer wells, fewer cores, and deeper targets. In undrilled basins one of our strongest tools is still a solid outcrop analog to predict what we cannot see in the seismic.
Looking Forward
Airborne and Ground Based LIDAR Integrated Digital Elevation Models
The image in Figure 5-3 is of the greater Austin area surveyed in early 2000 showing a 0.5 meter DEM color coded to elevation. Figure 5-4 (courtesy of the Center for Space research) is an IKONIS satellite image (one meter resolution) of the UT campus draped over the ALTM DEM (Figure 5-3). The image in Figure 5-5 is a larger scale window of the intersection in the foreground of Figure 5-4. The detail of the sides of buildings and data beneath underpasses is missing from airborne photos and surveys because they are line of sight instruments that cannot see under objects they can not fly under. The utility of a ground-based instrument (especially one with mm resolution) can clearly be understood from the limitations airborne only surveys encounter. A distant hope is the eventual integration of multi-or hyper-spectral scanners for ground surveys at high resolution and moderate cost.
Programming and comments by viewers
We are currently in the process of writing programs that allow us to process these types of data at a higher resolution faster, cheaper, and more accurately. The primary limitation with LIDAR research is hardware and software availability. There are few, if any, “off the shelf” software packages that are capable of handling tens of gigabytes of 3D data smoothly. Any comments or suggestions are more than welcome one this topic or anything related to this presentation. Please contact the senior author at his email address ([email protected]) |

 Figure 1-5. Ground-based LIDAR instrument.
Figure 1-5. Ground-based LIDAR instrument.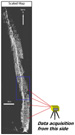 Figure 2-1. Map view of Ainsa 2 outcrop,
showing the general outcrop trend.
Figure 2-1. Map view of Ainsa 2 outcrop,
showing the general outcrop trend. Figure 2-5. The two images illustrate
perspective correction possibilities with use of LIDAR, along with index
map of Ainsa quarry.
Figure 2-5. The two images illustrate
perspective correction possibilities with use of LIDAR, along with index
map of Ainsa quarry. Figure 2-6. Photo mosaic (upper) taken from
the same perspective in Ainsa quarry as the ILRIS 3D data (lower).
Figure 2-6. Photo mosaic (upper) taken from
the same perspective in Ainsa quarry as the ILRIS 3D data (lower). Figure 2-7. Images of the same outcrop as that
in
Figure 2-7. Images of the same outcrop as that
in Figure 3-2. Another view of the stratigraphic
section in Guadalupe Canyon containing the channel complex--to
illustrate that ILRIS 3D acquires image data in a direct line of sight.
Figure 3-2. Another view of the stratigraphic
section in Guadalupe Canyon containing the channel complex--to
illustrate that ILRIS 3D acquires image data in a direct line of sight. Figure 3-4. Blown-up image of the “100-foot
Channel” point-cloud dataset, along with close-up view of individual x,
y, z, and intensity points displayed with a grayscale color bar.
Figure 3-4. Blown-up image of the “100-foot
Channel” point-cloud dataset, along with close-up view of individual x,
y, z, and intensity points displayed with a grayscale color bar. Figure 3-6. Conglomeratic channel fill,
Solitary Channel, Southern Spain. Photo (upper left); ILRIS 3D intensity
image (upper right); Same intensity image draped onto the TIN digital
terrain model (lower right).
Figure 3-6. Conglomeratic channel fill,
Solitary Channel, Southern Spain. Photo (upper left); ILRIS 3D intensity
image (upper right); Same intensity image draped onto the TIN digital
terrain model (lower right).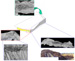 Figure 3-7. Solitary Channel outcrop, Southern
Spain: photograph, images, and block diagram.
Figure 3-7. Solitary Channel outcrop, Southern
Spain: photograph, images, and block diagram. Figure 4-2.
Victorio Canyon, with outline of the area of the north-facing canyon
wall that was scanned.
Figure 4-2.
Victorio Canyon, with outline of the area of the north-facing canyon
wall that was scanned. Figure 4-3.
Photograph of the north-facing canyon wall, Victorio Canyon, where data
were acquired in February, 2002.
Figure 4-3.
Photograph of the north-facing canyon wall, Victorio Canyon, where data
were acquired in February, 2002. Figure 5-2. Photograph of the operation of a
ground-based LIDAR instrument.
Figure 5-2. Photograph of the operation of a
ground-based LIDAR instrument. Figure 5-5. A larger scale window of the
intersection in the foreground of the image in
Figure 5-5. A larger scale window of the
intersection in the foreground of the image in