GCSpectral Balancing Aids Seeing Faults More Clearly*
Satinder Chopra¹ and Kurt J. Marfurt²
Search and Discovery Article #41594 (2015)
Posted March 20, 2015
*Adapted from the Geophysical Corner column, prepared by the authors, in AAPG Explorer, March, 2015, and entitled "A Delicate Balance: Seeing Faults More Clearly". Editor of Geophysical Corner is Satinder Chopra ([email protected]). Managing Editor of AAPG Explorer is Vern Stefanic. AAPG © 2015
¹Arcis Seismic Solutions, TGS, Calgary, Canada ([email protected])
²University of Oklahoma, Norman, Oklahoma
Spectral decomposition of seismic data helps in the analysis of subtle stratigraphic plays and fractured reservoirs. The different methods used for decomposing the seismic data into individual frequency components within the seismic data bandwidth serve to transform the seismic data from the time domain to the frequency domain – and generate the spectral magnitude and phase components at every time-frequency sample.
The spectral amplitude and phase components are analyzed at different frequencies, which means essentially interpreting the subsurface stratigraphic features at different scales. More recently, another important attribute that could be generated during spectral decomposition has been introduced, and is referred to as the voice component at every time-frequency component. For more details of this attribute, see Geophysical Corner article Autotracking Horizons in Seismic Records – Search & Discovery Article #41489.
The voice component at any individual frequency, say 30 Hz, is obtained by cross-correlating the seismic amplitude data with the mother wavelet (such as the Morlet wavelet), centered at 30 Hz with a frequency width of 30 Hz on either side. Thus the bandwidth of the voice component increases as the frequencies increase from the lower end to the higher end of the bandwidth. One may consider the process to be equivalent to applying a narrow band pass filter centered at 30 Hz to the data, but having some narrow bandwidth around on both sides.
|
♦General statement ♦Figures ♦Examples ♦Method ♦Conclusions
♦General statement ♦Figures ♦Examples ♦Method ♦Conclusions
♦General statement ♦Figures ♦Examples ♦Method ♦Conclusions
♦General statement ♦Figures ♦Examples ♦Method ♦Conclusions |
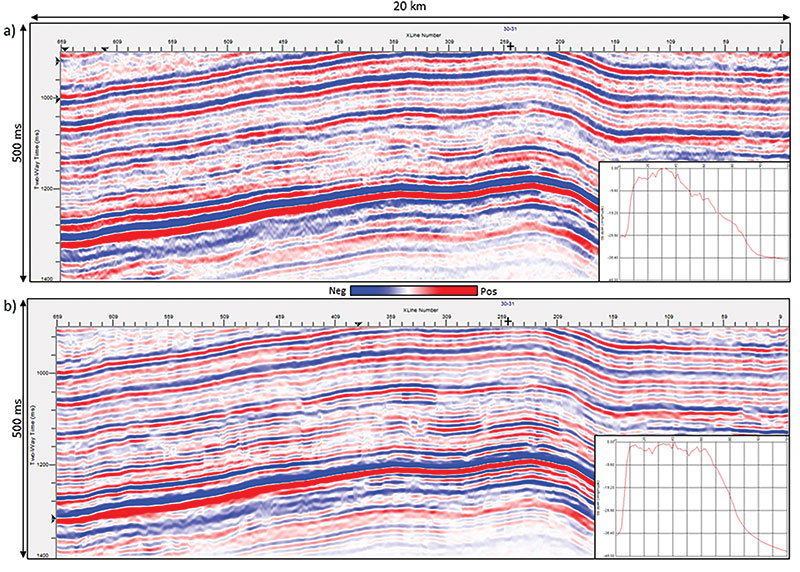
We show an example of a voice component section in Figure 1, along with its amplitude spectrum. Such voice components offer more information that could be processed and interpreted. We have focused on interpretational objectives of spectral decomposition in our earlier articles in the Geophysical Corner (Spectral Decomposition's Analytical Value – Search & Discovery Article #41260, and Extracting Information from Texture Attributes – Search & Discovery Article #41330) and demonstrated our examples pertaining to channels and other stratigraphic features. In this article our examples focus on faults and fractures. In Figure 2 we show a segment of a seismic section from a 3-D seismic volume from northern-central Alberta, Canada. The equivalent sections from the spectral magnitude, phase component, and the voice component at 65 Hz are shown in Figures 2b, c and d respectively. Notice that the vertical discontinuity information is not clearly seen on the spectral magnitude, but rather on the phase component. The voice component combines both attributes and nicely delineates the discontinuities. This observation could be exploited to our advantage by either interpreting the discontinuity information as such, or by running a discontinuity attribute, such as coherence, on the voice component volume. Traditionally, the spectral component magnitudes at different dominant frequencies have been utilized for obtaining detailed perspectives on stratigraphic objectives. As an example, the thickness of a channel is correlated with the spectral magnitude. More detailed information on seismic geomorphology can be gained by visualizing data at specific frequencies, or combining data with different frequencies using RGB color schemes. Another conclusion that one can have is that if the input data are spectrally balanced, or if its frequency bandwidth is somehow extended, the resulting volumes could lead to higher discontinuity detail. We focus on this aspect in this article. In another Geophysical Corner article (Spectral Balancing Can Enhance Vertical Resolution – Search & Discovery Article #41357), Marfurt and Matos described an amplitude-friendly method for spectrally balancing the seismic data. In this method, the data are first decomposed into time frequency spectral-components. The spectral magnitude is averaged over all the traces in the data volume spatially and in the given time window, which yields a smoothed average spectrum. Next, the peak of the average power spectrum also is computed. Both the average spectral magnitude and the peak of the average power spectrum are used to design a single time-varying spectral balancing operator that is applied to each and every trace in the data. As a single scalar is applied to the data, the process is considered as being amplitude friendly. Figure 3 shows segments of a seismic section and its equivalent section after spectral balancing. The individual amplitude spectral before and after are shown as insets. Notice that after spectral balancing the seismic section shows higher frequency content and the amplitude spectra is flattened. Encouraged with the higher frequency content of the data, we run Energy Ratio coherence on the input data as well as the spectrally balanced version of the data. The results are shown in Figures 4a, b and 5a, b, where we notice the better definition of the NNW-SSE faults as well as the faults/fractures in the E-W direction on the coherence run on spectrally balanced version. Finally, we run the spectral decomposition on spectrally balanced version of the input seismic data, and put the voice components through to Energy Ratio coherence computation. In Figures 4c, d, e and 5c, d, e we show time slices and horizon slices at different levels from the 65, 75 and 85 Hz frequency volumes. Notice the clarity in the definition of the discontinuities on both sets of displays. Such data lead to better interpretation of the discontinuities than carrying out the same exercise of the input data. The conclusions that one can draw from the foregoing examples is that spectral balancing of seismic data, when performed in an amplitude-friendly way, leads to higher frequency content – which in turn exhibits detailed definition of faults and fractures. Such discontinuity information can be interpreted better on coherence displays in the zone of interest. Coherence attribute computation performed on spectral decomposition after spectral balancing, or on the voice components at higher frequencies yields higher detail with regard to the faults and fractures. |