![]() Click to view article in PDF format.
Click to view article in PDF format.
Oil Shales: Their Shear Story*
Jyoti Behura1, Michael L. Batzle1, Ronny Hofmann2 and John Dorgan1
Search and Discovery Article #40379 (2009)
Posted March 16, 2009
*Adapted from oral presentation at AAPG Annual Convention, San Antonio, TX, April 20-23, 2008
1Geophysics, Colorado School of Mines, Golden, CO.
2Shell International Exploration and Production, Houston, TX. ([email protected])
Organic-rich shales house large untapped amounts of hydrocarbons. In-situ recovery of these hydrocarbons involves thermal cracking and steamflooding of these reservoirs which changes its physical properties, and shear properties in particular. We measure, within the seismic band, the complex shear modulus (and thus also the attenuation) of two oil shale samples, one rich in organic content and the other low in organic content.
Both the kerogen-rich and the lean shale show a weak dependence of modulus and Q on frequency. Their properties can be effectively considered frequency independent within the seismic band. These shales, however, show a dramatic change in shear-wave velocity and attenuation with temperature. Their shear moduli and Q decrease with melting of the kerogen, but with the subsequent loss of some of the kerogen, both shear moduli and Q increase. The magnitudes of these changes along the direction of the bedding and perpendicular to the bedding differ, which makes velocity  anisotropy
anisotropy and attenuation
and attenuation  anisotropy
anisotropy potentially valuable attributes. The velocity
potentially valuable attributes. The velocity  anisotropy
anisotropy and attenuation
and attenuation  anisotropy
anisotropy of the shales can change significantly with temperature, in some cases by more than an order of magnitude. The amount of kerogen content in a shale also influences the velocity and attenuation. The more the organic content, the lower is the shear modulus and the higher is the attenuation.
of the shales can change significantly with temperature, in some cases by more than an order of magnitude. The amount of kerogen content in a shale also influences the velocity and attenuation. The more the organic content, the lower is the shear modulus and the higher is the attenuation.
|
|
Introduction
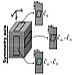
A vast unexploited source of hydrocarbons is oil shales, i.e., shales rich in kerogen. The Schlumberger Oilfield Glossary defines kerogen as "the naturally occurring, solid, insoluble organic matter that occurs in source rocks and can yield oil upon heating." The US Office of Naval Petroleum and Oil Shale Reserves estimates there are some 1.6 trillion barrels of oil contained in oil shales around the world, with 60-70% of reserves (1.0-1.2 trillion barrels) in the United States. Technical challenges and environmental concerns, however, hinder their exploitation. Environmental considerations, for example, have rendered surface-mining unfeasible. This calls for in-situ recovery, which poses new technical challenges. The most promising in-situ project is being carried out by Shell Oil Company under the name of the Mahogany Research Project in Colorado, which uses electrical heating. A heating element is lowered into the well and allowed to heat the kerogen over time, slowly converting it into oils and gases, which are then pumped to the surface. Seismic techniques can play an important role in monitoring changes in these oil shale reservoirs. Heating and steamflooding will change physical properties such as modulus, Measurements are carried out using a shear rheometer. The rock sample is clamped at both ends, and measurements are conducted with the sample dry and under no lateral confining stress. A sinusoidal torsional strain is applied on one end, and the resulting stress is recorded on the other end, which is fixed. The experiment is schematically shown in Figure 1. When a viscoelastic material is subjected to a sinusoidally varying strain, a steady state will be reached when the resulting stress is also sinusoidal, with the same angular frequency, but with a phase lag of δ, which is a measure of attenuation of that body (O'Connell and Budiansky, 1978). For an elastic material, δ=0, and for a viscous fluid, δ can approach π/2, while δ for a viscoelastic body has a value between these two limits. Note that the minimum value for Q depends on how it is defined. For extremely lossy materials, Q derived from phase angle can approach 0 (O'Connell and Budiansky, 1978). The in-phase part of the stress, σ', gives the "real" or the "storage" modulus, G', and the out-of-phase part of the stress gives the "imaginary" or "loss" modulus, G", G' = σ'/ε, .........(1) G" = σ"/ε. .........(2) The quality factor, Q, which is inversely proportional to the attenuation coefficient, is defined as (O'Connell and Budiansky, 1978) Q ≈ 1/tanδ = 2π W/W = G'/G". ......(3) where W is the maximum elastic stored energy during a cycle of loading at the frequency under consideration and W is the energy dissipated per cycle. We analyzed two samples of shale from the same formation (Green River Formation, Colorado) with different amounts of organic content, one with ≈30% and the other with ≈5% organic content. We also examined the influence on shear wave velocity Dynamic mechanical analysis of the shales was carried out for temperatures ranging from 30°C to 350°C at 20°C increments, with the frequency varying from 0.01 to 80 Hz in increments of 0.1 on the log10 scale. All the measurements are carried out in the linear viscoelastic regime, at a constant strain of 8x10-5, under a variable applied axial stress which does not allow the sample to expand vertically. This is similar to reservoir recovery conditions where the shale is heated but its expansion is restricted. Figures 3a-b show the real part, C'55, and inverse quality factor, 1/Q55, respectively, for the kerogen-rich shale, and Figures 3c-d are for Č66. Velocity dispersion is relatively weak in these kerogen-rich shales evident from the small change in C'55 and C'66 with frequency. Both storage moduli (C'55 and C'66) increase with frequency, even though the increase is small with the most noticeable change in the vicinity of 150°C. At low frequencies, the shales have time to undergo deformation (relaxed state), which reduces the storage modulus, while with increasing frequency, the time available for the particles to move decreases, making the shale stiffer. Within the seismic bandwidth, however, dispersion is essentially absent and Q can be safely assumed as a constant. So the observed attenuation likely is predominantly caused by frictional dissipation owing to relative motions at grain boundaries, or at interfaces between mineral and kerogen surfaces. Both moduli (C'55 and C'66) and attenuation (1/Q55 and 1/Q66) show a marked change with temperature. Figure 4 shows a comparison of the moduli and quality factors (along the two directions) for 0.3 Hz. C'55 and C'66 both drop sharply with increasing temperature up to ≈200°C, probably caused by the liquefaction of kerogen in the shale. Carcione (2000) suggested that Č55 is mostly controlled by the isotropic kerogen in the shales while Č66 is dominated by the clay in the layering. This explains the greater drop in C'55 than that in C'66. As the kerogen melts, it facilitates relative sliding between the clay layers, thus making the shale softer and more lossy as a result of increased frictional sliding. This lowers the quality factors, as seen in Figure 4b, where they drop from ≈40 at room temperature to below 5 at ≈150°C. With further increase in temperature, the kerogen is altered and partially expelled, thereby increasing the stiffness (Figure 4a) and decreasing any frictional losses as well, as evident from the increase in Q, as seen in Figure 4b. It is especially convenient to analyze the above changes in terms of the γQ = (Q55-Q66)/Q66 .........(4) As mentioned above, the magnitude of the effect of melting and evaporation of kerogen on C'55 and C'66 is different. This translates to a significant change in γ as seen in Figure 4a. As the kerogen melts, C'55 drops significantly compared to C'66, resulting in a jump in γ. With further increase in temperature, kerogen starts evaporating, which results in a drop in γ as the shale becomes less compliant. As with velocity γ and γQ for the whole frequency and temperature range are shown in Figures 5a and 5b, respectively. SH-wave velocity This experiment also shows the contribution of layering to the C'55 for the lean shale under confining axial stress is shown in Figure 6a. The general trends for lean shale are similar to those for the kerogen-rich shale. The magnitudes of lean-shale moduli, however, are larger than those of the organic-rich shales because the larger clay content in the lean shale increases its modulus. This might be used as a distinguishing factor between lean and kerogen-rich shales. Velocity dispersion is weak (Figures 6a), especially within the seismic band. Attenuation is also weakly dependent on frequency. This weak frequency dependence at intermediate temperatures (around 150°C) of attenuation implies that friction may be the dominant attenuation mechanism. Later, we will give more evidence in favor of frictional attenuation. Additional experiments, however, are necessary to find out if other mechanisms, such as "squirt flow" of fluids and viscous relaxation, are playing important roles. With increase in temperature, till about 200°C, C'55 drops more rapidly than does C'66. This fall in the storage moduli is most probably due to the liquefaction of the small amount of kerogen sandwiched between the clay layers. As discussed earlier in the previous section, any change to the kerogen would influence Č55 much more than Č66, which explains the greater drop in C'55. Below 200°C, the liquefaction of kerogen not only softens the rock, bringing down C'55, but also decreases the quality factor, Q55 sharply. This is because the liquid kerogen facilitates sliding, thereby decreasing the efficiency of transfer of mechanical energy between clay particles and increasing frictional loss. Like the kerogen-rich shales, these effects can be better seen by the changes in To test if friction is the dominant loss mechanism, we conducted another set of measurements to find C'55 under constant axial stress, results for which are shown in Figure 6b. If friction were indeed the dominant loss mechanism, two major changes would occur. First, C'55 would decrease in general. Second, for temperatures above 200°C, just as when the kerogen is lost, C'55 under constant axial stress would continue to decrease. This is because under constant axial stress, after loss of some kerogen, the voids left behind are retained, which decreases C'55 further. In contrast, under increasing axial stress, the voids are occupied by the expanding clay minerals as the rock is not allowed to expand. Both these effects can be seen by comparing Figures 6a and 6b, which support friction as the dominant attenuation mechanism. In-situ recovery of oil from oil shales involves thermal processes which melt the kerogen. These changes, therefore, should have a more pronounced effect on the shear-wave properties of the shales than the P-wave properties. So a study of the shear properties of these rocks is more attractive than the study of their bulk properties and thus makes acquisition of multicomponent seismic data all the more important. Our shear property measurements, as a function of temperature, should be representative of the conditions encountered during in-situ thermal cracking and steamflooding of oil shale reservoirs. Moreover, as our measurements encompass the seismic band, they should be more representative of the seismic properties of oil shales in the field. The strong temperature dependence of the mechanical properties of oil shales makes 4D-9C seismic analysis promising. The melting of kerogen can bring down the shear velocity significantly, by as high as five times in some cases. Their quality factor can also drop by a factor of 10 when going from room temperature to ≈150°C. So reservoir areas affected by heat should show a noticeable drop in velocities accompanied by significant increase in attenuation. Seismic data can be exploited to estimate the physical state of the rock, thus the local temperature. As has already been used in many studies, the direction and extent of the steam front can also be detected from seismic data. Oil shales have an additional property to be exploited - The original kerogen content in a shale also influences the behavior of the shale with temperature. From our study, we see that lean-shales have higher storage moduli and higher Q than more organic rich shales. Also the change in velocity Balkulin, A., 2003, Intrinsic and layer-induced vertical transverse isotropy: Geophysics, v. 68/5, p. 1708-1713. Carcione, J.M., 2000, A model for seismic velocity and attenuation in petroleum source rocks: Geophysics, v. 65/4, p. 1080-1092. O'Connell, R.J., and B. Budiansky, 1978, Measures of dissipation in viscoelastic media: Geophysical Research Letters, v. 5/1, p. 5-8. Thomsen, L., 1986, Weak elastic Zhu, Y., and I. Tsvankin, 2006, Plane-wave propagation in attenuative transversely isotropic media: Geophysics, v. 71/2, p. T17-T30. |