Mechanics of Natural Hydraulic Fracturing – Review and Introduction
Alfred Lacazette
Consulting Geologist, 1302 Waugh Dr., Suite 637, Houston, Texas 77019, U.S.A.
telephone: 713-503-0543; fax: 281-754-4821; email: [email protected]
URL: http://www.NaturalFractures.com
Subsurface fluid-flow and natural rock fracture development are intimately coupled:
- Fluid pressure can drive joints (extensional fractures) even in the absence of tectonic movements.
- Fluid pressure sensitizes rocks to faulting (shear fracturing).
- The PVT relations and chemical properties of fluids are a critical control on the rate, driving stress, and amount of fracture propagation.
- Fractures allow rapid, even catastrophic, fluid-flow across and/or parallel to stratigraphic boundaries.
- Fluid-flow changes the neostress (in-situ stress-state) of the rock mass, the stress perturbations caused by fractures in the rock mass, and the mechanical equilibrium of individual fractures.
- Fracture mediated fluid-flow affects mineral equilibria because it changes fluid pressure, temperature and composition. Disequilibria causes host-rock dissolution and/or precipitation of minerals within fractures and the rock matrix, which affect fluid-flow within the fractures.
This conference is about such feedbacks, their effects on petroleum systems, and especially on practical exploration and exploitation methodology. This presentation attempts to provide a basic understanding of the linkage between fluid pressures, neostress and fracturing, and a set of equations for exploratory calculations. A set of handouts will be provided giving simple key equations (as below), graphs, and figures to facilitate discussions, back-of-the-envelope calculations, and arm-waving during the conference. The talk will focus on the graphs and photographs of natural examples of these phenomena. Natural hydraulic extensional fracturing (NHF) is given particular attention for two reasons:
- NHF is the most common mechanism of joint (natural extensional fracture) formation, and joints are one of the most common and pervasive fracture types.
- Although NHF is normally ignored in migration studies, NHF-mediated migration is common, can move fluid more rapidly than capillary flow, can be rapid or even catastrophic, and episodic or continuous. Unlike capillary flow, NHF-mediated flow rates can change rapidly in response to stress changes and/or fluid production by maturation and/or dewatering because the process is dominated by the PVT relations of the migrating/maturing fluids and the mechanical properties and stress-state of the rock. Lithologies that present a barrier to capillary flow may not be a barrier at all to NHF-mediated flow, and vice-versa.
Natural hydraulic fracturing
Faulting (shear fracturing). A pore-fluid pressure increase can cause shear fracturing under deviatoric stresses (stress differences) that are much too small to cause shear fracturing in dry rock. This effect occurs both during slip of pre-existing mechanical discontinuities (such as beds, joints and older faults) and during generation of new faults in virgin rock. Although this effect is well understood and discussed in undergraduate structural geology texts, explosive brecciation resulting from pore-pressure assisted shear fracturing is a less well-known phenomenon. Explosive brecciation occurs as follows: Fault-slip decreases the stresses in an envelope around the slipped fault-patch. Explosive brecciation occurs when the stress-drop is sufficiently large relative to the pore-pressure that a volume is produced around the fault in which pore fluid pressure exceeds rock strength. The excess pore-pressure shatters the rock. Such brecciation can become a self-perpetuating process because brecciated fault zones are highly permeable so that high-pressure fluids move from depth to the fault tip resulting in more fault-slip and brecciation. This brecciation process is described and documented by Phillips (1972). Explosive brecciation into extensional rhombochasms is a similar, but distinct, type of fluid-driven brecciation that occurs when a slip event suddenly extends a fluid-filled irregularity on the fault surface thereby dropping the fluid-pressure in the cavity much faster than it can flow out of the porous wall rock.
Jointing (extensional fracturing). Extensional fractures always develop perpendicular to the least principal tectonic stress. An artificial hydraulic fracture, such as those used to stimulate wells, propagates when the fluid pressure within the fracture
(Pf) exceeds the sum of the least principal tectonic stress (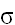 3r , compression is positive) and the inherent resistance of the rock to propagation of the fracture (S). In other words, when:
3r , compression is positive) and the inherent resistance of the rock to propagation of the fracture (S). In other words, when:
Pf > S + 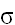 3r
(1)
3r
(1)
Such fractures can develop naturally when a fracture carrying fluid from a deep, high-pressure reservoir rapidly propagates upward. In such cases the fluid pressure in the fracture is much greater than the pore fluid pressure in the host rock. However, Equation 1 ignores the pore-pressure of the host rock. Including host-rock pore-pressure in Equation 1 gives:
Pf > S + 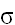 3r
+
3r
+ 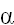 Pp
(2)
Pp
(2)
where Pp is the pore-pressure in the host rock and 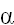 (Biot’s Constant or the Poroelastic Constant) expresses the contribution of pore-pressure to the stress of the solid skeleton of the rock (Engelder & Lacazette, 1990; Lacazette & Engelder, 1992; Engelder, 1992). Important points about the variables:
(Biot’s Constant or the Poroelastic Constant) expresses the contribution of pore-pressure to the stress of the solid skeleton of the rock (Engelder & Lacazette, 1990; Lacazette & Engelder, 1992; Engelder, 1992). Important points about the variables:
- Biot’s constant ranges from zero to one, is one for unconsolidated material and is less than one for any consolidated material. In geological materials
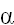 ranges from ~0.98 for some “unconsolidated” sediments to < 0.1 for very low porosity rocks. (The primary non-time-dependent controls on
ranges from ~0.98 for some “unconsolidated” sediments to < 0.1 for very low porosity rocks. (The primary non-time-dependent controls on
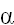 are porosity, compressibility of the solid constituents and grain bonding.)
are porosity, compressibility of the solid constituents and grain bonding.) - The resistance of the host rock to a specific fracture is a function of the fracture’s size, shape, and the material properties that control resistance to fracture. Note that strength is not a material property, however S can be thought of as a strength term. An upper bound for S is given by:
S = KIC / YC½
(3)
Where KIC is the critical fracture toughness (a material property); Y is a dimensionless constant that expresses
the fracture geometry, position, and loading condition; and c is the size parameter of the fracture. In rocks
KIC ranges from 0.4 to 2.8 MPa m½. For a flat, circular, disk-shaped crack embedded in an infinite solid Y=1.13 and c is the crack radius in meters. In most geologic situations
S is substantially less than this upper bound because of subcritical crack propagation, which is strongly affected by chemical environment and is strongly time-dependent. This time-dependence is one important reason that rocks are weak over geologic time. Subcritical propagation will be covered in detail by Jon Olson.
Now let’s evaluate Equation 2 for an unfractured, maturing source-bed in a tectonically stable environment. Let’s assume that:
- Tectonically stable means that
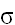 3r
is constant on the time-scale of interest.
3r
is constant on the time-scale of interest. - The minimum stress is horizontal. This is the case for most of the earth’s crust most of the time especially along passive continental margins and in gradually subsiding basins.
- S is constant.
- The fracture for which we are calculating a propagation pressure (Pf) is a favorably-oriented (= perpendicular to
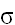 3) pore in the rock that is at minimum a few dozen grain diameters across. Such imperfections are numerous in rocks and are produced by fossils, clasts, sedimentary processes, and other causes. Field studies show that joints typically nucleate on flaws ranging from a few tenths to several tens of millimeters in diameter.
3) pore in the rock that is at minimum a few dozen grain diameters across. Such imperfections are numerous in rocks and are produced by fossils, clasts, sedimentary processes, and other causes. Field studies show that joints typically nucleate on flaws ranging from a few tenths to several tens of millimeters in diameter.
Hydrocarbon maturation and clay dewatering alone can produce volumes of fluid many times larger than the pore volume of the host rock. This fluid is relatively incompressible so that Pp increases rapidly if capillary flow cannot keep pace with fluid production. The fluid pressure increases uniformly throughout the pore space of the rock because maturation occurs over geologic time, which is equivalent to saying that Pf=Pp prior to fracture initiation. The left side of Equation (2) can easily exceed the right side even though Pf=Pp because Pf is the pore pressure, but the pressure term on the right side is a fraction of the pore pressure while the other terms on the right side are constants. The fracture starts propagating as soon as the failure condition is met, and propagation causes S to decline exponentially with size and ultimately become 10% or less of its original value when fracture has grown a meter or two long. This catastrophic decline of S with size increases the disequilibrium of Equation (2) so that the fracture continues to grow. The volume increase of the fracture causes the fluid pressure to drop within the fracture so that fluid flows from the matrix to the fracture until the total volume increase of the system brings the fracture back into a stable equilibrium. However, stress varies rapidly with depth so that a fracture that remains connected to a sufficiently large reservoir can spontaneously ascend many kilometers in a relatively short period of time. Also, natural rock fractures do not reclose perfectly and therefore remain avenues of flow even after reclosure by a pressure decline. For these reasons, NHF-mediated migration can respond rapidly and sensitively to changes in fluid volume and pressure.
If we consider Equation 2 for a stable fluid pressure during a tectonic stress drop then we find that a natural hydraulic fracture is produced before the rock goes into true tension no matter how low the value of Pp, which suggests that most joints are natural hydraulic fractures.
The PVT behavior of the fluid system is also a critical control on fracture initiation and propagation. For example:
- Gas can produce three orders of magnitude more fracture volume for a given pressure drop than brine or liquid petroleum because of its greater compressibility. Many or most cases of cyclic joint propagation may result from a gas drive. (Lacazette & Engelder, 1992)
- Consideration of the work of fracturing indicates that the Joule-Thompson coefficient (µ = dT/dP) of a gas is an important parameter because this value affects the amount of work that is available from a fluid and µ varies significantly for methane mixtures with P, T, and composition in the PTX range of industrial interest. (Lacazette & Engelder, 1992)
- Methane-brine solubility relations show that methane generation can cause catastrophic fluid-pressure increases with very small changes in composition in a fixed pore-volume rock mass so that NHF is highly favored at the moment that a brine becomes saturated with methane during generation.
The talk will focus on illustrating these and other hydraulic fracture phenomena with graphs, field photos, specimens and subsurface data, including a case where migrating hydrocarbon-bearing fluids caused the rocks to change color thereby clearly revealing the flow paths and a cyclic, gas-driven joint. Equations will be confined to this abstract and the handout. The handout will provide equally simple equations for first-order computations of fracture volume, flow-rate, earth stress computations including the effects of poroelasticity and other quantities.
This material will be made available on my website, NaturalFractures.com.
Engelder, T. and Lacazette, A., 1990, Natural hydraulic fracturing: p. 35 - 43 in N. Barton and O. Stephansson (editors): Rock Joints: Proceedings of the international symposium on rock joints. Loen, Norway. June 4-6, 1990: A.A. Balkema, Brookfield.
Engelder, T., 1992, Stress regimes in the lithosphere. Princeton University Press, 457 p..
Lacazette, A. and Engelder, T., 1992, Fluid-driven cyclic propagation of a joint in the Ithaca Siltstone, Appalachian Basin, New York: p. 297 - 323 in B. Evans and T.-F. Wong (editors): Fault Mechanics and Transport Properties of Rocks; a festschrift in honor of W. F. Brace: Academic Press, San Diego.
Phillips, W.J., 1972, Hydraulic fracturing and mineralization: Journal of the Geological Society of London, v. 128, p. 337-359.
Copyright © 2004. The American Association of Petroleum Geologists. All Rights Reserved.
