Click to view
article in PDF format.
GC
Reflection
Events and Their Polarities Defined by the Hilbert Transform*
Bob Hardage1
Search and
Discovery Article #40564 (2010)
Posted July 30, 2010
*Adapted from the Geophysical Corner
column, prepared by the author, in AAPG Explorer, July, 2010, and entitled
“Complex Traces: There’s an ‘App’ for That”. Editor of Geophysical Corner is
Bob A. Hardage ([email protected]). Managing Editor of AAPG Explorer is
Vern Stefanic; Larry Nation is Communications Director. Please see closely related article “Instantaneous Seismic Attributes Calculated by the Hilbert Transform”, Search and Discovery article #40563.
1Bureau of Economic Geology, The University of Texas at
Austin ([email protected])
General Statement
Previously we introduced
the concept of a complex seismic trace (“Instantaneous Seismic Attributes Calculated by the Hilbert Transform”, Search and Discovery article #40563);
here we’ll show how a complex trace provides a rigorous way to set the
boundaries of data windows associated with distinct seismic reflections – and
we’ll define the polarities of each of those reflection events. This complex
trace application is important because it is necessary to determine the
polarity of every reflection event that spans a layered system in order to
determine whether impedance increases or decreases from layer to layer – which
in turn provides insight into the lithology, porosity and type of pore fluid in
each rock layer.
The
principal problem involved in determining the polarity of a seismic reflection
event is the challenge of deciding what part of the seismic response represents
the reflection event. Questions that have to be answered include:
· Where does
the reflection event start and stop?
· How many
peaks and troughs are embedded in the reflection event?
· Which peak or trough of a reflection event
should be used to define reflection polarity?
The
amplitude-envelope function determined from a complex seismic trace provides a
way to define the start time, stop time, wavelet character and polarity of
overlapping – but distinct – reflection events.
Figure Captions
|
|
|
 General statement
Figures
Reflection events
Reflection polarity
General statement
Figures
Reflection events
Reflection polarity
General statement
Figures
Reflection events
Reflection polarity
General statement
Figures
Reflection events
Reflection polarity
|
Defining Reflection
Events
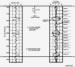
An
example seismic trace, its complex-trace equivalent and the associated
amplitude envelope are shown as Figure 1:
the amplitude envelope of a complex seismic trace is an oscillating function
that has alternating maxima and minima. The data window between two
successive minima of an amplitude-envelope function defines a distinct packet
of seismic energy. Terms that have been used to describe this interval
between successive amplitude-envelope minima are energy packet, wavelet
packet and reflection event. Once you equate the term “reflection event” with
energy packet (or with wavelet packet), you can then ask the question: “How
many reflection events occur between time coordinates A and B on Figure 1?”
You
will get the definitive answer “13.” A wavelet packet such as any of those
defined on Figure 1 may be a reflection from
a single interface, or it may be a composite of several reflections from
closely spaced interfaces. In either case, a wavelet packet represents the
shortest-time concentration of reflection of energy that can be recognized in
a seismic response. Because amplitude-envelope minima can be determined
numerically after an amplitude envelope is calculated, the start time, stop
time and time extent of a reflection event can be defined with mathematical
rigor, as shown by each of the labeled “events” on Figure
1, and do not have to be left to interpreter judgment. The basic
seismic wavelet that is embedded in the seismic trace on the left of Figure 1 is shown in the center part of the figure.
A reader can compare this wavelet with its associated reflection trace on the
left of the display to attempt to decide how many reflection events exist
across the time interval A to B. In classroom and workshop exercises, people
have tended to conclude that the number of reflection events ranges from a
low of five or six to a high of 17 or 18. Using the mathematical concept of
amplitude-envelope minima to define the boundaries of a reflection event, the
correct answer is 13 reflection events (right-hand panel) as already stated.
Defining Reflection
Polarity
When
a reflection event is defined by this energy packet concept, the polarity of
the reflection event can be defined as the algebraic sign of the real-trace
extremum (either peak or trough) that is closest to the maximum of the
amplitude-envelope that encompasses the energy packet. Using this concept,
the polarity of reflection events 5 and 10 on Figure
1 are positive, and the polarities of reflection events 7 and 12 are
negative. Thus a complex-trace allows seismic reflection polarity to be
defined with the same mathematical rigor that defines the time extent of each
reflection event.
A
second illustration of energy packets being used to define distinct
reflection events and their polarities is provided as Figure 2. In this case, there are excellent examples of energy
packets distinguishing overlapping reflection events (events 7 and 8, and
events 11 and 12) and defining the data windows spanned by faint,
low-amplitude reflections (events 2 and 3).
Return
to Top. Copyright © AAPG. Serial rights given by author. For all other rights contact author directly.
|
Print this page
