![]() Click to view article in PDF format.
Click to view article in PDF format.
GCInstantaneous  Seismic
Seismic Attributes Calculated by the Hilbert Transform*
Attributes Calculated by the Hilbert Transform*
Bob Hardage1
Search and Discovery Article #40563 (2010)
Posted July 17, 2010
*Adapted from the Geophysical Corner column, prepared by the author, in AAPG Explorer, June, 2010, and entitled “Thin Is In: Here’s a Helpful Attribute”. Editor of Geophysical Corner is Bob A. Hardage ([email protected]). Managing Editor of AAPG Explorer is Vern Stefanic; Larry Nation is Communications Director. Please see closely related article “Reflection Events and Their Polarities Defined by the Hilbert Transform”, Search and Discovery article #40564.
1Bureau of Economic Geology, The University of Texas at Austin ([email protected])
Geological interpretation of  seismic
seismic data is commonly done by analyzing patterns of
data is commonly done by analyzing patterns of  seismic
seismic amplitude,
amplitude,  phase
phase and frequency in map and section views across a prospect area. Although many
and frequency in map and section views across a prospect area. Although many  seismic
seismic attributes have been utilized to emphasize geologic targets and to define critical rock and fluid properties, these three simple attributes – amplitude,
attributes have been utilized to emphasize geologic targets and to define critical rock and fluid properties, these three simple attributes – amplitude,  phase
phase and frequency – remain the mainstay of geological interpretation of
and frequency – remain the mainstay of geological interpretation of  seismic
seismic data.
data.
Any procedure that extracts and displays any of these  seismic
seismic parameters in a convenient and understandable manner is an invaluable interpretation tool. A little more than 30 years ago, M.T. Taner and Robert E. Sheriff introduced the concept of using the Hilbert transform to calculate
parameters in a convenient and understandable manner is an invaluable interpretation tool. A little more than 30 years ago, M.T. Taner and Robert E. Sheriff introduced the concept of using the Hilbert transform to calculate  seismic
seismic amplitude,
amplitude,  phase
phase and frequency instantaneously – meaning a value for each parameter is calculated at each time sample of a
and frequency instantaneously – meaning a value for each parameter is calculated at each time sample of a  seismic
seismic trace. That Hilbert transform approach now forms the basis by which almost all amplitude,
trace. That Hilbert transform approach now forms the basis by which almost all amplitude,  phase
phase and frequency attributes are calculated by today’s
and frequency attributes are calculated by today’s  seismic
seismic interpretation software
interpretation software
| |||||||||
|
|
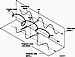
The action of the Hilbert transform is to convert a
These two traces combine to form a complex trace z(t), which appears as a helix that spirals around the time axis. The projection of complex trace z(t) onto the real plane is the actual
The orientation angle Ф(t) that defines where vector a(t) is pointing (Figure 2) is defined as the
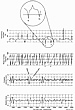
The calculation of these three interpretation attributes – amplitude,
Taner, M.T. and Robert E. Sheriff, 1977, Application of Amplitude, Frequency, and Other Attributes to Stratigraphic and Hydrocarbon Determination: Section 2. Application of
Copyright © AAPG. Serial rights given by author. For all other rights contact author directly. |