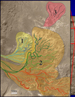
Martian Deltas and the Origin of Life*
By
Janok P. Bhattacharya1
Search and Discovery Article #40203 (2006)
Posted July 10, 2006
*Adapted from AAPG Distinguished Lecture, 2006.
![]() Click to view presentation
in PDF format (21.3 mb).
Click to view presentation
in PDF format (21.3 mb).
or Right click; then click "Save Target As" to download.
1University of Houston ([email protected])
There remains significant debate as to whether there were persistent water flows, significant precipitation and standing water bodies during the early Noachian history of Mars. Recent Mars Global Surveyor (MGS) Mars Orbiter Camera (MOC) images of meandering channels associated with a Noachian-age, lacustrine delta within Holden NE Crater show evidence for persistent water flows.
The topmost layer shows clear evidence of meandering streams associated with four depositional lobes. The channels record a complex history of migration, avulsion and bifurcation, forming a distributive pattern with up to 5 orders of branching. Several channels show a distinct transition from initially straight, to highly sinuous followed by classic chute cutoffs.
Relatively smooth, and more brightly reflective layers deeper in the crater fill may represent more-flat lying lacustrine bottom sets, and could speculatively be evaporitic. The transition from smooth lower layers that lack channel belts, to straight channels to meandering channels suggest a progressive evolution of the sedimentary fill.
Our analysis of the surface features, as well as estimates of accumulation rates of the underlying 150 meters of strata within the crater fill, suggests that Holden NE Crater may have contained a lake that persisted for a few thousand to possibly as long as a few million years. This supports the hypothesis that early Mars was both warmer and wetter during the Noachian. In addition, these sediments represent a probable watery habitat that should be investigated for evidence of possible extinct Martian life.
|
|
When did life appear on earth? Could life have appeared anywhere else in the solar system or universe? Where and how to look for evidence of life in the “universe”? –Need to find habitable environments.
History of Life on Earth (Figure 1) 4.6 billion years to 544 million years. • Represents 90% of all of the history of the earth. • Referred to as the Cryptozoic Eon. – “hidden life” • Used to be called Azoic Eon – “without life”
Single-celled Archea(ancient bacteria) appear in the fossil record very soon after rigid, cool earth crust formed. •Why so soon? –Chemicals available –Water available –Lots of excess energy to power chemical reactions
Experiments on Origin of First Cells •1950's and 1960's experiments combined atmospheric gases (NH3, H2, CH4, water, electricity and heat to produced amino acids, formadehydeand cyanide. –Demonstrated abiotic processscould make precursors of life. •Further experiments demonstrated that drying and re-wetting of these organic compounds could produce cell-like membranes and simple proteins. –Led to shallow water “primordial soup”theory. •But organic compounds in shallow pools would have been instantly destroyed by ultraviolet radiation and oxidation in young, thin atmosphere. •Life may have evolved far from sunlight in deep oceans around geothermal vents
•Archaebacteria are the most primitive fossil life forms –Likely ancestors of all life. •Primitive Archaebacteria are hyperthermophiles that thrive in boiling water. –Modern Archaebacterialive in deep-sea volcanic vents. •Many Archaebacteria feed directly on sulfur (chemoautotrophs). –Archean life probably arose in deep oceans hydrothermal, volcanic vents that would have dotted the ocean floor near rifting zones. –Vents provide: •chemical and heat energy, •abundant chemical and mineral compounds, including sulfur •protection from oxygen and ultraviolet radiation.
Prokaryotic archaebacteria and eubacteria are dominant. –Eubacteria form stromatolites.(photosynthetic). –More common in upper Archean as shallow water shelves began to form along margins of early.continents. –Archean is the age of pond-scum. Molds of individual bacterial cells found in Precambrian cherts.
Evolution of Eukaryotes: c.1.8 Ga (Figure 3)
•Probably began as a symbiotic relationship between different prokaryotes •Early eukaryotes “ate”but could not digest a cell which became a mitochondria. •Plant-like eukaryotic ancestors “ate”chlorophyll-bearing cyanobacteria. •Once eukaryotes evolved, multi-cellular and colonial forms proliferated.
Appearance of Metazoans: 570 Ma •Nothing more complicated on earth than bacteria for 4 Billion Years! •First metazoans evolve about 570 million years ago.
Precambrian and Phanerozoic Life (Figures 4 and 5)
Precambrian-dominated by bacteria and algae: The Age of Pond Scum!
Paleozoic--95% of all marine species went extinct --250 Million Years ago2
Mesozoic--most of the creatures went extinct --65 million years ago
Which event is unusual in Earth History •Origin of Archea? –Inevitable? •Rise of metazoans? –Took a longtime •Rise of vertebrates? –Followed soon after metazoans •Appearance of language? –Only happened once, in 1 species in 4.6 billion years!
•Origin of Archea? –Inevitable? –Look for evidence in solar system •Origin of Language –SETI project
Comparison of Planets (Figure 6)
•Because of temperature gradient, outer planets are icy and inner planets are rocky. •Large planets also retain atmospheric gas because of higher gravity.
Searching for habitable environments on Mars: “Follow the water” •Sedimentary Environments –Several have been found –Mars is a very layered planet •Hydrothermal Environments –None identified to date (no active thermal events). •Environments associated with groundwater or ice. –2007 Phoenix Mission will sample polar ice.
Mean Radius: 3388.0 Km Mass: 0.108 (Earth=1) Gravity: 0.380 (Earth=1) Orbit Period: 686.98 (Earth Days) Rotation Period: 1.026 (Earth Days) Atmosphere: 8mb (Mostly Co2) –1/100th Of Earth’s Atmosphere! Temperature: 215°K (-65°C)–It’s Colder Than Canada! Conclusion –Mars is probably presently a dead planet –H.G. Wells, Orson Welles, and Stephen Spielberg are probably wrong.
•Mars may have been hotter and wetter in early history. •Escape velocity of Mars much lower than earth, so atmosphere has long since escaped. •Could life have evolved on early Mars? •Evidence for water compelling. •Present NASA Missons have found evidence for water that could indicate potential habitats for life. –“Follow the water”
•Noachian: 4.5Ba -3.5Ba –Heavy bombardment •Hesperian: 3.5 -2.0Ba –Moderate bombardment •Amazonian: 2.0Ba –present –Light bombardment •Mars is tectonically inactive and has been that way for most of its history. •Near complete record of Archean.
Searching for Evidence of Ancient Water laid deposits: Crater Lakes (Figures 8 and 9)
•Jarosite–KFe3(SO4)2(OH)6 –an uncommon mineral on Earth, which forms in dilute sulfuric acid in ground water. –Probably formed in an acidic lake or an acidic hot springs environment. •Heamatite“blueberries” –Fe203 –Small (mm-diameter) concretions. –Probably formed in groundwater and later weathered out.
Ripple Cross Lamination (Figures 11 and 12)
Ripples in Meridiani Planum •Rippled patterns suggest a standing body of water. •Cross-lamination is diagnostic of ripple shapes formed under a current of water --and not wind. •Mineralogy also indicates alternating humid to arid evaporiticconditions. •Area sometimes covered by shallow water and sometimes dry, such as in a playa lake.
---NASA Asks, 'Did Rivers Once Run on Mars?' Newly seen details in a fan-shaped apron of debris on Mars may help settle a decades-long debate about whether the planet had long-lasting rivers instead of just brief, intense floods. Pictures from NASA's Mars Global Surveyor orbiter show eroded ancient deposits of transported sediment long since hardened into interweaving, curved ridges of layered rock.
•How long-lived was drainage basin? •How was drainage basin carved? –Rainfall? –Groundwater sapping? •Caused by bolide impacts that melt groundwater
Modeling of Martian Geomorphology (Howard, 2004, especially 2005) Impacted surface Fluvial erosion Eolian reworking Initial cratered surface Surface after groundwater sapping Initial surface with eolian reworking Surface after groundwater sapping Models versus reality
Evidence of rainfall (Figures 13, 14, and 15)
Lack of craters in drainage headwaters suggests rainfall, rather than groundwater melting from bolides. Meandering valleys require long- term flows, rather than single catastrophic meltwater floods.
Features of Crater Fill (Figures 16, 17, and 18)
Multiple channels. •Downstream decrease in channel width. •Distributive channel pattern •Straight to meandering, single thread channels.
Martian Delta Lobes (Figures 19, 20, 21, 22, and 23)
Records complex history of fluvial avulsion and channel migration. •Downstream bifurcation suggests a distributive system. •No obvious reworking by waves or tides.
Coarse-grained channel belt deposits are held high. –Finer-interchannel(floodplain) sediment is eroded by wind. –Inverted geomorphology. •Channel belt surface is severely pock-marked, suggesting an extremely old (Noachian) age. –Over 3 Ga.
•Channels about 100m wide. •Cross-cutting relationships. •Channels wander, meander, and avulse. –Scroll bars represent “frequent”floods. –Avulsions represent “infrequent”major-floods. –How frequent???
•Original straight channel becomes sinuous and unstable and experiences a classic chute cutoff. •11 avulsions sweeping across the delta plain. –How frequent?
•Older channels are straight and then become more sinuous. •Younger channels overlie older channels. •Clear bifurcation downstream, suggesting distributary channels.
Delta versus Fan (Figures 24, 25, and 26)
•Alluvial fans are common on Mars. •Numerous, straight to braided shallow channels. •Strongly fan-shaped. •Correlate with small drainage areas. •Debris flows and landslides are also common on Mars. •Braided rivers are also common in Martian outwash valleys and northern plains. –these are very different from singe-thread, meandering channels in the Eberswalde delta. •Highly organized single-thread, straight to meandering channels. •Lack of debris flows or sheetflood deposits. •Lack of braided channels–indicate lower slopes or lower discharge than might be expected on an alluvial fan.
Estimating duration of the delta (Figures 27 and 28)
•Deltaic versus fan numbers considered more likely –No vegetation on Mars, but floodplain may have been frozen much of the year: stable floodplain? –Assume avulsion period of 100-500 years? •11 avulsions = 1100 to 5500 years for topmost layer. •Examine edge of outcrop to get thickness. –150 m thick •Note lighter deeper layers –Prodelta bottomsets? –Evaporites? •Outcrops about 150m high. •1100 -5500 years for upper layer. •150m x 1mm/year = 150,000 years for entire feature.
Conclusion (Figures 29 and 30)
•Long-lived delta. •Complex, dynamic history –Countless scroll-bar flood events –11 avulsions in top layer –Feature may have formed over 10,000 to 100,000 years. •Clearly not due to one major bolide-induced catastrophic groundwater melt episode. •It was probably raining on Mars during the Archean. •Fluvial deposits and probable delta deposit on Mars. •Preserve early sedimentary history. •Candidate for preserving fossil evidence of life (biosignatures).
Selected BibliographyBhattacharya, J.P., Payenberg, T., Lang, S., and Bourke, M., 2005, River Deltas in Crater Lakes on Early Mars: Search and Discovery Article #110026 (2005). Bridge, J.S., 2003, Rivers and Floodplains; Forms, Processes, and Sedimentary Record: Blackwell, Oxford, U.K., 491 p. Hoffman, P.F., 1976, Environmental diversity of Middle Precambrian stromatolites, in Walter, M.R., ed., Stromatolites: Developments in Sedimentology 20, Elsevier, Amsterdam, p. 599-612. Howard, A.D., 2004, Simple non-fluvial models of planetary surface modification, with application to Mars: Lunar and Planetary Science Conference XXXV, Abstract 1054. James, N.P., 1984, Shallowing-upwards sequences in carbonates, in Walker, R.G., ed., Facies Models, Second Edition: Geoscience Canada, St. Johns, Newfoundland, Reprint Series 1, p. 213-228. Jerolmack, D.J., D.M. Mohrig, M.T. Zuber and S. Byrne, 2004, A minimum time for the formation of Holden Northeast fan, Mars:, Geophys. Res. Lett., v. 31 (doi:10.1029/2004GL021326, 2004). Kargel, J.S, Kirk, R.L, Fegley, B, Treiman, A.H. 1994. Carbonate - sulfate volcanism on Venus?: Icarus. v. 112, p. 219-252. Lewis, K., and O. Aharonson, 2004, Stratigraphic analysis of the distributary fan in Holden NE crater using stereo imagery (Abstract #2083 of poster #8051): 2nd conference on Mars (www.lpi.usra.edu/meetings/earlymars2004/pdf/8051). Malin, M.C., and K.S. Edgett, 2003, Evidence for persistent flow and aqueous sedimentation on early Mars: Science, v. 302, p. 1931-1934 (doi:10.1126/science.1090544) (When connecting to this hyperlink, select your browser if requested). Moore, J.M., A.D. Howard, W.E. Dietrich, and P.M. Schenk, 2003, Martian layered fluvial deposits: Implications for Noachian climate scenarios: Geophys. Res. Lett. v. 30 (doi:10.1029/2003GL019002). Schopf, J.W. 1968, Microflora of the Bitter Springs Formation: Journal Paleontology, v. 42, p. 651-688. Sepkoski, Jr., J. John, 1981, A Factor Analytic Description of the Phanerozoic Marine Fossil Record: Paleobiology, v. 7, no. 1, p. 36-53.
•Co-authors –Tobi Payenberg(University of Adelaide) –Simon Lang (Woodside Petroleum) –Mary Bourke (Planetary Science Institute) •Alan Howard (University of Virginia) •James Reilly (NASA) •Robert E.Sheriff(University of Houston) |