![]() Click to view article in PDF format.
Click to view article in PDF format.
GC3-D Design Philosophy – Part 3: Is  Stacking
Stacking Fold Acceptable?*
Fold Acceptable?*
Bob Hardage1
Search and Discovery Article #40663 (2010)
Posted December 17, 2010
*Adapted from the Geophysical Corner column, prepared by the author, in AAPG Explorer, November, 2010, and entitled “Next Step: Is  Stacking
Stacking Fold Acceptable?”. Editor of Geophysical Corner is Bob A. Hardage ([email protected]). Managing Editor of AAPG Explorer is Vern Stefanic; Larry Nation is Communications Director. Click for remainder of series: Part 1 Part 2 Part 4
Fold Acceptable?”. Editor of Geophysical Corner is Bob A. Hardage ([email protected]). Managing Editor of AAPG Explorer is Vern Stefanic; Larry Nation is Communications Director. Click for remainder of series: Part 1 Part 2 Part 4
1Bureau of Economic Geology, The University of Texas at Austin ([email protected])
This article is the third of a four-article series – this topic considers Part 3 and Part 4 labeled on the Figure 1 flow chart of 3-D seismic design methodology.
 Stacking
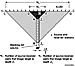
Stacking fold is the number of field traces that are summed during data processing to create a single image trace positioned at the center of each bin. At any
fold is the number of field traces that are summed during data processing to create a single image trace positioned at the center of each bin. At any  stacking
stacking bin coordinate, the
bin coordinate, the  stacking
stacking fold inside the bin varies with depth. Referring to Figure 2, when a
fold inside the bin varies with depth. Referring to Figure 2, when a  stacking
stacking bin is centered about a deep reflection point B, the
bin is centered about a deep reflection point B, the  stacking
stacking fold is a maximum at depth B because the largest number of source and receiver pairs can be utilized to produce individual reflection field traces inside the bin.
fold is a maximum at depth B because the largest number of source and receiver pairs can be utilized to produce individual reflection field traces inside the bin.
The number of source-receiver pairs that can contribute to the image at B is typically confined to those source and receiver stations that are offset horizontally from B a distance that is no larger than depth Z2 to reflection point B. Thus, distances CE and EG shown on Figure 2 are each equal to Z2.
Using this offset criterion to determine the number of source-receiver pairs that contribute to a seismic image at any subsurface point, the  stacking
stacking fold at depth Z2 would be N2 – because N2 unique source-receiver pairs can be found that produce distinct field traces reflecting from point B.
fold at depth Z2 would be N2 – because N2 unique source-receiver pairs can be found that produce distinct field traces reflecting from point B.
When the  stacking
stacking bin moves to a shallower depth Z1, the
bin moves to a shallower depth Z1, the  stacking
stacking fold decreases to a smaller number N1 – because only N1 source-receiver pairs generate field traces that reflect from A and still satisfy the geometrical constraint that the source-receiver pairs are offset a distance DE (or EF) or less that does not exceed depth Z1.
fold decreases to a smaller number N1 – because only N1 source-receiver pairs generate field traces that reflect from A and still satisfy the geometrical constraint that the source-receiver pairs are offset a distance DE (or EF) or less that does not exceed depth Z1.
In a 3-D context,  stacking
stacking fold is the product of in-line
fold is the product of in-line  stacking
stacking fold (the fold in the direction that receiver cables are deployed) and cross-line
fold (the fold in the direction that receiver cables are deployed) and cross-line  stacking
stacking fold (the fold perpendicular to the direction that receiver cables are positioned). Defining F as 3-D
fold (the fold perpendicular to the direction that receiver cables are positioned). Defining F as 3-D  stacking
stacking fold, FIL as in-line fold and FXL as cross-line fold, this principle leads to the design equation:
fold, FIL as in-line fold and FXL as cross-line fold, this principle leads to the design equation:
(1) F = FIL x FXL.
To build a high-quality 3-D image, it is critical to not only create a proper  stacking
stacking fold across the image space but also to ensure the traces involved in that fold have a wide range of offset distances and azimuths. Equation 1 provides no information about the distribution of source-to-receiver offset distances or azimuths that are involved in a
fold across the image space but also to ensure the traces involved in that fold have a wide range of offset distances and azimuths. Equation 1 provides no information about the distribution of source-to-receiver offset distances or azimuths that are involved in a  stacking
stacking fold. If it is critical to know the magnitudes and azimuth orientations of source-receiver offsets, then commercial 3-D design software must be used.
fold. If it is critical to know the magnitudes and azimuth orientations of source-receiver offsets, then commercial 3-D design software must be used.
Offset analysis is a topic that goes beyond the scope of this discussion, which is structured to provide simple explanations of the basic principles of 3-D seismic design. All discussions of 3-D  stacking
stacking fold will be based totally on equation 1. It is the simplicity of this equation that makes it appealing to use to explain to non-geophysicists how
fold will be based totally on equation 1. It is the simplicity of this equation that makes it appealing to use to explain to non-geophysicists how  stacking
stacking fold and 3-D recording geometry link together.
fold and 3-D recording geometry link together.
|
2-D vs 3-D
In 2-D and 3-D acquisition geometry, in-line
● The number of active receiver channels.
● The ratio of the source-station interval and the receiver-station interval.
Specifically, in-line
(2) FIL = (1/2) (Number of receiver channels) X [(receiver-station interval)/ (source-station interval)].
In 2-D seismic profiling, the source-station interval is usually the same as the receiver-station interval, making the ratio term in the square brackets equal to unity. However, in 3-D profiling, the source-station spacing along a receiver line is the same as the source-line spacing, which is several times larger than the receiver-station spacing. For example, if the receiver-station spacing is 110 feet, and the interval between the source lines is 1,320 feet, then there is a source station every 1,320 feet along each receiver line – and the square bracket term in equation 2 has a value of (1/12).
The in-line fold for 3-D data acquisition is thus considerably less than it is for 2-D recording geometries. In this hypothetical example, it is 12 times less. Cross-line
(3) FXL = (1/2) (Number of receiver lines in recording swath).
The last step in the 3-D design procedure (Part 4 of Figure 1) is to compare the designed
There are several ways to answer this question. The ideal situation is to have access to 3-D seismic data previously recorded near the prospect area. If those data have good signal-to-noise character, then one should simply define the
If the signal-to-noise character of these pre-existing 3-D data is not acceptable, a higher
(4) 3D
This is a statement of a commonly observed condition that 3-D
If the calculated EXPLORER
Copyright © AAPG. Serial rights given by author. For all other rights contact author directly. |