 Click to view article in PDF format.
Click to view article in PDF format.
An Analytical Formulation of
Seismic-derived  Resistivity
Resistivity *
*
By
Denny Merkurius F. Mendrofa1 and Bambang Widarsono2
Search and Discovery Article #40245 (2007)
Posted June 30, 2007
*Adapted from extended abstract prepared for presentation at AAPG Annual Convention, Long Beach, California, April 104, 2007
1Premier Oil Ltd, Jakarta, Indonesia
2Lemigas Jakarta, Jakarta Selatan, Indonesia
Recent
developments in seismic petrophysics have shown that efforts to establish
methods used for deriving water saturation (Sw) from seismic usually
meet an end as empirical approaches and/or in the use of various kinds of
artificial intelligence. The quest for establishing reliable methods for
estimating beyond-well water saturation data has always been underway in the
last one or two decades. Many investigators have spent efforts in trying to find
reliable ways to use seismic data to serve the purpose. This paper presents a
theoretical formulation of  resistivity
resistivity functions using which it becomes possible
that
functions using which it becomes possible
that  resistivity
resistivity data is extracted from seismic data. This work is basically a
reformulation of the previously introduced concept of linking theory of acoustic
wave propagation and water saturation models. In this theoretical work, Gassmann
is still used as the acoustic velocity model while Poupon and Hossin water
saturation models are used to represent formation rocks containing laminated
shale and dispersed shale, respectively.
data is extracted from seismic data. This work is basically a
reformulation of the previously introduced concept of linking theory of acoustic
wave propagation and water saturation models. In this theoretical work, Gassmann
is still used as the acoustic velocity model while Poupon and Hossin water
saturation models are used to represent formation rocks containing laminated
shale and dispersed shale, respectively.
The work presented in this paper
is basically to link primary wave velocity (Vp) and
acoustic impedance (AI) to other parameters such as rock  true
true
 resistivity
resistivity (Rt), a parameter known to be very sensitive
to variation in fluid saturation. Widarsono and Saptono (2003, 2004)
provide laboratory verifications and first field trial with some
degree of success. However, certain assumptions (i.e.
constant/uniform porosity) in the theoretical formulation were still
adopted in the above works, which in turn reduced the validity of
the resulting formula produced and used. With this reformulation, it
is hoped that a more robust model/formula of
(Rt), a parameter known to be very sensitive
to variation in fluid saturation. Widarsono and Saptono (2003, 2004)
provide laboratory verifications and first field trial with some
degree of success. However, certain assumptions (i.e.
constant/uniform porosity) in the theoretical formulation were still
adopted in the above works, which in turn reduced the validity of
the resulting formula produced and used. With this reformulation, it
is hoped that a more robust model/formula of  resistivity
resistivity as a
function of acoustic impedance (Rt = f(AI)) is
achieved, hence a more reliable
as a
function of acoustic impedance (Rt = f(AI)) is
achieved, hence a more reliable  resistivity
resistivity could be extracted from
seismic-derived acoustic impedance.
could be extracted from
seismic-derived acoustic impedance.
In brief, Gassmann theory (Gassmann, 1951) is actually a modification of Hooke’s theory (elastic deformation theory) and provides a theory for acoustic wave velocity in porous media. For a porous and fluid saturated elastic medium, the P-wave equation was modified into

where Pd is the P-wave modulus for the rock frame (or dry rock), and f(Kf ) is the function of the incompressibility of the fluid in the pore spaces. The P-wave modulus for the dry rock can be expressed, in turn, by

and the function f(Kf ) by
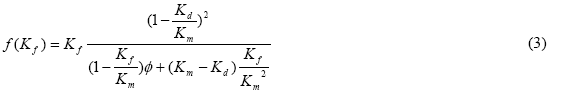
The subscripts d, f, and m refer to the rock frame (or the dry rock,), fluid, and rock matrix. The rb and f(Kf) in Equations (1) and (3), respectively, contain porosity (f) and water saturation (Sw). When these two equations are rearranged a water saturation function can be established. See Mendrofa (2006) for a full derivation of the water saturation function.
On the other hand, the relation
between Rt and Sw is more
straightforward. This is  true
true since for brine-saturated clean
sedimentary rocks the total electrical conductivity is solely
governed by the amount of the brine within the pore system. The
electric current simply flows through the tortuous pore system that
is filled continuously by the brine and completely ignores the
non-conductive hydrocarbon fraction and rock matrix.
since for brine-saturated clean
sedimentary rocks the total electrical conductivity is solely
governed by the amount of the brine within the pore system. The
electric current simply flows through the tortuous pore system that
is filled continuously by the brine and completely ignores the
non-conductive hydrocarbon fraction and rock matrix.
For the purpose of this formulation work two shaly-sand models, instead of Archie model as used in Widarsono and Saptono (2003, 2004), Poupon and Hossin models have been chosen. The reason for the choice of the two models are their relative simple form and the fact that the two models were derived to accommodate the presence of laminated shale (Modified Simandoux) and dispersed shale (Hossin).
The Poupon model (Poupon et al, 1954) is expressed in the form of

while the Hossin model (taken from Dresser Atlas, 1982) is expressed in the form of

with n, Vsh,
Rsh, m, a, and Rw
are saturation exponent, shale fraction, shale  resistivity
resistivity ,
cementation factor, tortuosity, and formation water
,
cementation factor, tortuosity, and formation water  resistivity
resistivity ,
respectively. The models in Equations 4 and 5 will introduce Rt
into the Gassmann acoustic velocity model.
,
respectively. The models in Equations 4 and 5 will introduce Rt
into the Gassmann acoustic velocity model.
It is now the turn to underline that water saturations in any mathematical expressions should have the same general meaning physically, which is basically ‘a part of a rock’s pore space that is occupied by formation water’. Therefore, it is fundamentally correct to state that

where Sw(petrophysics) is Sw in any water saturation models commonly known in log analysis (e.g., Modified Simandoux and Hossin models) and Sw(Gassmann) is Sw in the Gassmann acoustic velocity model.
Following Equation (6), and after
all required mathematical arrangements, a  resistivity
resistivity function of
function of

is obtained for porous rocks containing laminated shale, and

is obtained for porous rocks
containing dispersed shale. Equations (7) and (8) are essentially
the solution of Rt = f(AI). The variable of AI is
contained in variables of I and J (i.e., I and J are functions of
AI) whereas variables H and T also represent some simple
mathematical expressions that are temporary established to simplify
Equations (7) and (8). See Mendrofa (2006) for full derivations of
the two  resistivity
resistivity functions.
functions.
For trial using the two equations,
a set of log suites has been obtained from a Sumatran production
well penetrating two gas bearing shaly-sands. Density and acoustic
logs are available to derive acoustic impedance (AI =
rb
x Vp), gamma ray log for shale contents, whereas shallow
and medium depth  resistivity
resistivity logs are available to provide
environmentally corrected formation
logs are available to provide
environmentally corrected formation  resistivity
resistivity at investigation
depths relevant to acoustic and density logs. Data and other
information regarding the well and the two sands are obtained from
laboratory reports, study reports, as well as from local knowledge.
Summarily, the supporting data used in the works is:
at investigation
depths relevant to acoustic and density logs. Data and other
information regarding the well and the two sands are obtained from
laboratory reports, study reports, as well as from local knowledge.
Summarily, the supporting data used in the works is:
-
quartz sand density; rm = 2.648 gm/cc
-
oil density, rhc = 0.8 gm/cc
-
fresh water density; rw = = 1.0 gm/cc
-
shale density; rsh = 2.45 gm/cc
-
shale resistivuty; Rsh = 0.5 Ohm-m
-
tortuosity; a = 1.0
-
cementation factor; m = 2.3
-
saturation exponent; n = 1.76
-
formation brine
 resistivity
resistivity ; Rw = 0.693 Ohm-m @ 75oF or
0.27 Ohm-m @ reservoir temperature
; Rw = 0.693 Ohm-m @ 75oF or
0.27 Ohm-m @ reservoir temperature -
mud filtrate
 resistivity
resistivity ; Rmf = 17.5 Ohm-m @ 75oF or
6.92 Ohm-m @ 200oF (oil base mud)
; Rmf = 17.5 Ohm-m @ 75oF or
6.92 Ohm-m @ 200oF (oil base mud) -
rock matrix bulk modulus; Km = 40 Gpa
-
water bulk modulus; Kw = 2.38 Gpa
-
gas bulk modulus; Kg = 0.021 Gpa
-
rock dry bulk modulus; Kd = 0.24 Gpa
-
Vp/Vs ratio = 1.5 or s = 0.1 (homogeneous and isotropic quartz sandstone, according to Gregory, 1976)
Although the two sands are
gas-bearing in nature, but since the well was drilled using oil base
mud and as a matter of fact that the depth of investigation of
density and acoustic logs are shallow, the system is therefore oil –
water (i.e., water – mud filtrate). In consequence,  resistivity
resistivity values from shallow and medium depth
values from shallow and medium depth  resistivity
resistivity devices are taken
as the ‘observed Rt’ in the well.
devices are taken
as the ‘observed Rt’ in the well.
Figures 1-4 show comparisons between calculated  resistivity
resistivity values
versus observed values. In general, it can be clearly seen that the
two sets of
values
versus observed values. In general, it can be clearly seen that the
two sets of  resistivity
resistivity show similarity in trends; i.e., variation
in magnitudes with depth. The very difference between the two sets
is in the respective magnitudes. The observed
show similarity in trends; i.e., variation
in magnitudes with depth. The very difference between the two sets
is in the respective magnitudes. The observed  resistivity
resistivity values
tend to be significantly higher than the calculated ones. A vast
number of trials have been made to modify the supporting data within
the theoretically allowed ranges. Despite the trials, agreements in
magnitudes are not much better between the two sets. Indeed this can
be considered as a ‘setback,’ but nevertheless this work has started
a path of research that can be followed up in the future.
values
tend to be significantly higher than the calculated ones. A vast
number of trials have been made to modify the supporting data within
the theoretically allowed ranges. Despite the trials, agreements in
magnitudes are not much better between the two sets. Indeed this can
be considered as a ‘setback,’ but nevertheless this work has started
a path of research that can be followed up in the future.
|
Figure 1. Acoustic impedance log and synthetic |
|
|
Figure 2. Acoustic impedance log and synthetic |
|
|
Figure 3. Acoustic impedance log and synthetic |
|
|
Figure 4. Acoustic impedance log and synthetic |
References
Dresser Atlas, 1982, Well Logging and Interpretation Techniques: Dresser industries Inc., 211 p:.
Gassmann, F., 1951, Elastic waves through a packing of spheres: Geophysics, v.16, p. 673-685.
Gregory,A.R., 1976, Fluid saturation effects on dynamic elastic properties of sedimentary rocks: Geophysics, v. 41, p. 895-924.
Mendrofa, D.M.F., 2006,. An Analytical Derivation of
 Resistivity
Resistivity from Acoustic Impedance in Porous Elastic Media: M.S.
Thesis, University of Indonesia.
from Acoustic Impedance in Porous Elastic Media: M.S.
Thesis, University of Indonesia.
Poupon, A., Loy, M.E., and Tixier, M.P., 1954, A contribution to electrical log interpretation in shaly sands: Trans. AIME, v. 201, p. 138 – 145.
Widarsono, B., and Saptono, F., 2003,A new method for
obtaining inter-well  true
true
 resistivity
resistivity (Rt) from seismic data
– a field trial: Lemigas Scientific Contributions, no. 2/2003, p. 2-7.
(Rt) from seismic data
– a field trial: Lemigas Scientific Contributions, no. 2/2003, p. 2-7.
Widarsono, B.,
and Saptono, F., 2004,  Resistivity
Resistivity data from a seismic survey? An
alternative approach to assist inter-well water saturation mapping: SPE
Paper 87065, SPE Asia Pacific Conference on Integrated Modeling for
Asset Management, Kuala Lumpur, Malaysia, March 29-30.
data from a seismic survey? An
alternative approach to assist inter-well water saturation mapping: SPE
Paper 87065, SPE Asia Pacific Conference on Integrated Modeling for
Asset Management, Kuala Lumpur, Malaysia, March 29-30.
