![]() Click to view images in PDF format.
Click to view images in PDF format.
GC Seismic
Seismic Modeling and Imaging - Making Waves*
Modeling and Imaging - Making Waves*
By
Phillip Bording1 and Larry Lines2
Search and Discovery Article #40066 (2002)
*Adapted for online presentation
from the Geophysical Corner column in AAPG Explorer December, 2000,
entitled “ Seismic
Seismic Modeling Makes Waves,” and prepared by the authors.
Appreciation is expressed to the author, to R. Randy Ray, Chairman of the AAPG
Geophysical Integration Committee, and to Larry Nation, AAPG Communications
Director, for their support of this online version.
Modeling Makes Waves,” and prepared by the authors.
Appreciation is expressed to the author, to R. Randy Ray, Chairman of the AAPG
Geophysical Integration Committee, and to Larry Nation, AAPG Communications
Director, for their support of this online version.
1Consultant, Hazel Green, Alberta, Canada
2University of Calgary, Alberta ([email protected])
Exploration seismology essentially involves dealing with  seismic
seismic wave
equations. We record
wave
equations. We record  seismic
seismic waves, process digital
waves, process digital  seismic
seismic signals and
attempt to interpret and understand the meaning of these signals in
geological terms. Discontinuities in subsurface rock formations give
rise to
signals and
attempt to interpret and understand the meaning of these signals in
geological terms. Discontinuities in subsurface rock formations give
rise to  seismic
seismic reflections, or “echoes.” These signals provide us with
information about the location of geological structures and,
consequently, allow us to search for hydrocarbon traps.
reflections, or “echoes.” These signals provide us with
information about the location of geological structures and,
consequently, allow us to search for hydrocarbon traps.
The key to
successful  seismic
seismic exploration lies in deriving meaningful images of
subsurface geology. In order to do this, our computer imaging codes need
to use accurate mathematical descriptions of waves.
exploration lies in deriving meaningful images of
subsurface geology. In order to do this, our computer imaging codes need
to use accurate mathematical descriptions of waves.
|
|
Click here for
sequence of the snapshots of an expanding
Click here for sequence of Figure 3a and 3b.
Modeling
Our ability to
compute solutions of the elastic wave equation allows us to both model
and image · One is Newton's Second Law of Motion, which states that the acceleration of a body equals the force acting on the body divided by the mass of the body. · The other law is Hooke's Law of elasticity, which states that the restoring force on a body is proportional to its displacement from equilibrium. By combining these two laws, we obtain the elastic wave equation. In the simplest case of a homogeneous rock body, the wave equation is given by:
In the equation:
·
The symbol
· "u" is the wavefield. (If we are recording with hydrophones, we would consider pressure wavefields.) · "v" represents the wave velocity in the medium.
·
To compute
solutions numerically to the wave equation, we need to evaluate second
derivatives in space and time. This evaluation basically amounts to the
use of finite differences of the wavefield in space and time. If we set
up a stencil of points in the space and consider digital values of the
Figure 1 shows movie snapshots of wave propagation passing through
an earth model consisting of layers onlapping on a salt dome. This
allows us to model or simulate numerically the
An even more
useful application of
In order to
understand the ability of For this experiment, we could equivalently also consider the wave to be generated by a pulse that was initiated at the geologic reflector and traveled at half of the velocity of the medium to the receiver. This is the so-called “exploding reflector model.” which was an ingenious idea of the late Dan Loewenthal who pioneered its use in various migration algorithms.
Our ability to
image the subsurface geology would be made possible by “running the wave
propagation movie backward in time” for the exploding reflector
experiment. This would be achieved by moving the recorded Fortunately, we are able to "reverse-time propagate" wavefields by using the same wave equation computations as we used in forward modeling. Wavefields for the movie progressing backward in time satisfy the wave equation, just as waves progressing forward in time. For a brief historical note, it should be mentioned that this idea had an enormous practical use in Amoco's exploration of the Wyoming Overthrust Belt in the 1980s. Dan Whitmore of Amoco Research was probably the first to make widespread use of “reverse-time” migration in exploration geophysics - as evidenced by his examples of overthrust imaging and salt dome imaging, which were shown at the 1982 and 1983 SEG annual meetings. Reverse-time wave imaging or migration can be done via the following technique, as originally explained by three papers in 1983 produced by McMechan (1983), Whitmore (1983), and Baysal et al. (1983).
First of all,
consider recorded
Next, propagate
these The imaging method is as general as the form of the wave equation that is used. Almost all of the complexities of reverse-time wave equation migration in its various combinations of acoustic, elastic, 2-D, 3-D, anisotropic, multi-component forms have been described in several papers by George McMechan and his students at the University of Texas at Dallas (e.g., Wu and McMechan, 1998).
In order to
convince the explorationist of the power of reverse-time depth
migration, we examine the salt pillow model example shown in
Figure 3. The seismogram at the top of this figure is not
interpretable - except possibly for a few flat
In order to
unravel the
Summary
For real data,
depth migration is rarely this good due to the fact that we generally
have only estimates of the
We should not
give the impression that reverse-time migration is restricted to In essence, “making waves” to produce useful images is a worthwhile occupation in many scientific pursuits. Baysal, E., D.D. Kosloff, and J.W.C. Sherwood, 1983, Reverse time migration: Geophysics, v. 48, p. 1524-1524.. Fink, Mathias, 1999, Time-reverse acoustics: Scientific American, November 1999. McMechan, G., A, 1983, Migration by extrapolation of time-dependent boundary values: Geophysical Prospecting, v. 31, p. 413-420. Whitmore, N. Dan, 1983, Iterative depth migration by backward time propagation: SEG Abstracts, SEG International Meeting and Exposition, v. 1, p. 382-385.
Whitmore, N. Dan, and Larry R. Lines, 1986, Vertical Wu, Yafai, and G.A. McMechan, 1998, Wave extrapolation in the spatial wavelet domain with application to poststack reverse-time migration: Geophysics, v. 63, p. 589-600. |

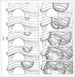 Figure 1. A
series of model snapshots of an expanding
Figure 1. A
series of model snapshots of an expanding  Figure 2. This
cartoon shows the
Figure 2. This
cartoon shows the 