![]() Click to view article in PDF format.
Click to view article in PDF format.
Three-Dimensional Prestack  Inversion
Inversion , Lobo Trend,
South Texas*
, Lobo Trend,
South Texas*
By
Phil Anno1, Mark Wuenscher1, Robert Corbin1, John Hooper1, and Frank Chlumsky2
Search and Discovery Article #10039 (2003)
*Adapted from “extended abstract” of presentation at AAPG Annual Meeting, March 10-12, 2002, Houston, Texas.
1Conoco Inc., Ponca City, Oklahoma
2Conoco Inc., Houston, Texas
We demonstrate the
difficulty with mapping a Lobo (Paleocene) hydrocarbon reservoir directly from
stacked  seismic
seismic
 data
data . A strong response in the stacked volume is ambiguous,
indicating either a large impedance contrast or a contrast in Poisson’s ratio.
. A strong response in the stacked volume is ambiguous,
indicating either a large impedance contrast or a contrast in Poisson’s ratio.
That is, stacking
of reflection amplitudes over offset (or reflection angle) incorporates
reflections from impedance perturbations with those due to a change in Poisson’s
ratio. Dipole sonic log  data
data indicate Poisson’s ratio, but not impedance,
distinguishes this particular Lobo reservoir from shale. The hydrocarbon
reservoir impedance is similar to that of encasing shales. On the other hand,
Poisson’s ratio decreases over 30% in the reservoir sand.
indicate Poisson’s ratio, but not impedance,
distinguishes this particular Lobo reservoir from shale. The hydrocarbon
reservoir impedance is similar to that of encasing shales. On the other hand,
Poisson’s ratio decreases over 30% in the reservoir sand.
In this paper, we
invert the prestack amplitudes of a 3-D  data
data volume to distinguish perturbations
in impedance from Poisson’s ratio perturbations. We may, therefore, recognize
and map this Lobo reservoir as a decrease in Poisson’s ratio accompanied by
little or no change in impedance.
volume to distinguish perturbations
in impedance from Poisson’s ratio perturbations. We may, therefore, recognize
and map this Lobo reservoir as a decrease in Poisson’s ratio accompanied by
little or no change in impedance.
|
|
Click here to view sequence of Figures 1 and 2 (P-wave impedance and Poisson’s Ratio logs).
The upper Paleocene to Eocene Wilcox Lobo trend is a major low-permeability natural gas producer of the Texas Gulf Coast, already yielding approximately 4.5 TCF of gas. Both structural and stratigraphic complexity can complicate exploration and exploitation of the Lobo trend. Multiple episodes of faulting and erosion can make sand correlation difficult from fault block to fault block. Previous
Lobo exploration tools consisted of open-hole logs and dipmeter Continuous improvements in 3-D acquisition and processing over the last ten years have positively impacted Lobo exploration and development success. Current 3-D stack volumes resolve much smaller slump blocks. This improved structural definition helps identify acreage that yields superior drilling results. Modern
dipole sonic log measurements through the Lobo section point to
Poisson’s ratio as a distinguishing reservoir property. Prestack imaging
and In this paper we directly image a Lobo reservoir by inverting amplitudes before stack. A signature decrease in Poisson’s ratio tracks the reservoir across faulting.
The well
One can
invert throughout the 3-D volume for perturbations in Poisson’s ratio,
along with impedance perturbations. This
Figures 3
and 4 give time slices of the resulting Though this
prestack R(q ) =A + Bsin2q + Csin2q tan2q + K (1) Equation (1) expresses reflectivity R as a function of incidence angleq. One derives this equation following the approaches taken by Bortfeld (1961), and Aki and Richards (1980). Shuey (1985) presented a similar approximation. Equation
(1) also sets the goal of our entire prestack Parameter A in equation (1) equates to a perturbation in impedance under the assumption of small perturbations. Parameter B is the source of information on Poisson’s ratio. It depends in part on the product of perturbations in both impedance and Poisson’s ratio. We
truncated equation (1) before parameter C for the
Equation (1) thus makes it clear that stacking of reflection amplitudes over angle incorporates reflections from impedance perturbations with those due to a change in Poisson’s ratio. The A -term contributes the former, the B -term the latter. A strong response in the stacked volume is therefore ambiguous in terms of rock properties.
Figures 6,
7 and 8 taken together document this ambiguity for the Lobo section. The
band of prominent reflections in the stack
Multiple
episodes of faulting and erosion in the Lobo trend can frustrate Dipole
sonic log
We thank
Peter Lellis for hisencouragement and initiative to apply prestack
Aki, K., and Richards, P.G., 1980, Quantitative seismology: Theory and methods: W.H. Freeman and Co. Bortfeld, R., 1961, Approximation to the reflection and transmission coefficients of plane longitudinal and transverse waves: Geophys. Prosp., v. 9, 485-503. Shuey, R.T., 1985, A simplification of the Zoeppritz equations: Geophysics, v. 50, p. 609-614.
|

 Figure 1.
P-wave impedance well log, coded according to log-derived lithology. The
legend provides the code.
Figure 1.
P-wave impedance well log, coded according to log-derived lithology. The
legend provides the code. Figure 2.
Poisson’s Ratio well log, coded according to log-derived lithology.
Figure 2.
Poisson’s Ratio well log, coded according to log-derived lithology. Figure 3. A
time slice through the impedance perturbation cube from 3-D prestack
Figure 3. A
time slice through the impedance perturbation cube from 3-D prestack
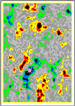 Figure 4. A
time slice through the Poisson’s Ratio perturbation cube from 3-D
prestack
Figure 4. A
time slice through the Poisson’s Ratio perturbation cube from 3-D
prestack  Figure 6.
An inline slice through the Poisson’s Ratio perturbation cube from 3-D
prestack
Figure 6.
An inline slice through the Poisson’s Ratio perturbation cube from 3-D
prestack  Figure 7.
An inline slice through the amplitude stack cube.
Figure 7.
An inline slice through the amplitude stack cube. Figure 8.
An inline slice through the impedance perturbation cube from prestack
Figure 8.
An inline slice through the impedance perturbation cube from prestack
