![]() Click to view article in PDF format.
Click to view article in PDF format.
GCAn 'Elastic Impedance' Approach*
Satinder Chopra1and Ritesh Kumar Sharma1
Search and Discovery Article #41082 (2012)
Posted November 12, 2012
*Adapted from the Geophysical Corner column, prepared by the author, in AAPG Explorer, October, 2012. Editor of Geophysical Corner is Satinder Chopra ([email protected]). Managing Editor of AAPG Explorer is Vern Stefanic; Larry Nation is Communications Director. AAPG©2012
1 Arcis Corp., Calgary, Canada ([email protected])
A detailed investigation of seismic amplitudes can yield information pertaining to lithological variation in subsurface sedimentary rock formations and the existence and extent of some hydrocarbon zones. This objective can be facilitated in a process called seismic inversion, which transforms seismic amplitudes into acoustic impedance values. In doing so, the seismic reflection response gets transformed into layered impedance response, which makes the interpretation of the lithological and fluid information more convenient – each transformed impedance trace can now be considered as an impedance log curve and the seismic volume as logs recorded in wells drilled at every seismic trace location. Just as the changes in the character of impedance log curves are indicative of changes in lithology, porosity and fluid content, similar changes seen on inverted impedance traces are interpretable of these properties in a lateral sense over an area and so over a volume.
Acoustic impedance inversion has now become an integral part of most interpretation projects today. While this is a beneficial tool for the seismic interpreter, acoustic impedance inversion is usually run on stacked seismic traces – that is, the individual prestack time migrated offset gathers are stacked and then transformed into impedance. To better exploit the fluid effects that manifest on prestack gathers as variation of amplitudes with offset or angle, prestack impedance inversion also can be carried out. Of course, it would take longer - and so the trade-off is usually between the cost, time and the method to be used.
|
|
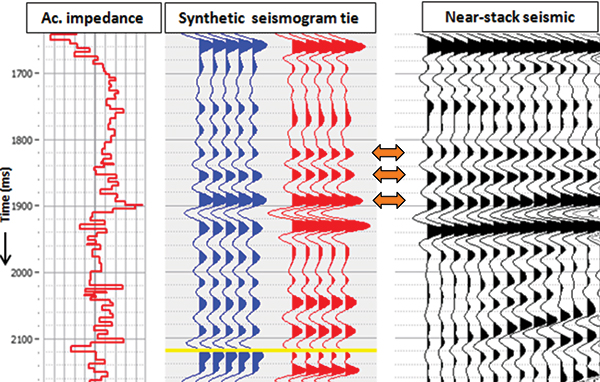
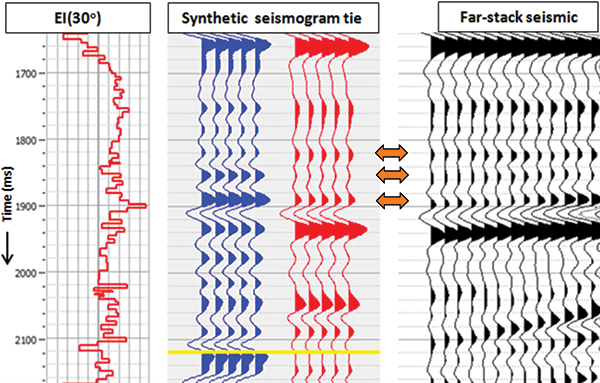
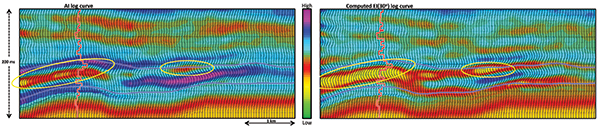
A simple way to examine the variations of amplitude as a function of offset is to generate the offset-limited seismic volumes, such as the near-, mid- and far-offset (or angle) volumes. Variations seen on these volumes in desired zones could then be indicative of the fluid information. For example, a low-impedance gas-sand sandwiched between shale would yield an increase of amplitude with offset. Such a variation can be detected on comparing the near-offset seismic volume with the equivalent far-offset volume, and noticing high amplitude anomalies on the latter corresponding to the gas samples. As amplitudes of the near-offset traces are related to the changes in acoustic impedance they can be calibrated with well log curves or synthetic seismograms. However, if a far-offset or a far-angle stack has to be calibrated with the log data or synthetic seismograms, there is no analogous set of log curves that could be used for the purpose. Back in 1999, Patrick Connolly from BP pointed this out and suggested the generalization of acoustic impedance for variable incidence angle using a linearized version of Zoeppritz equations. He called this "elastic impedance," and it provides the framework to calibrate and invert non-zero offset data. The elastic impedance approach is strongly dependent on the medium parameters (VP, VS, and density and angle of incidence), and so is often regarded as the rock attribute analog of acoustic impedance for varying angles of incidence. In actual practice, the CMP gather at the position of the well is picked up, different angle ranges are selected and angle stacks generated. Given the VP, VS and density log curves, the elastic impedance is calculated for different angles of incidence. The angle stack traces from the gather and those derived from the log curves (elastic impedance, or "EI") are compared for a visual assessment and interpretation. Another useful and meaningful display is the comparison of the acoustic impedance log curve with the elastic impedance curve at the far-angle that is admissible for the given data. In Figure 1, the acoustic impedance log is compared with the EI (30 degree) log curve for a discovery well from Colombia. The target is related to Eocene fluvial deposits, mainly composed of interbedded medium- to fine-grained quartz sandstones and claystones. The gas was detected during mud logging and on the electric log curve; however, the density and neutron curve crossover is not as high as expected, probably due to low saturation as well as its position. The saturation is expected to increase in the up-dip direction. Notice that there is a decrease of impedance at the gas-sand interface, and so it will show up as higher amplitudes on the seismic data. It may be mentioned that the elastic impedance values vary significantly with the incidence angle – and because of this, when elastic impedance logs have to be displayed alongside with or overlaid on acoustic impedance, they have to be scaled in such a way that the EI values for all angles fall in the range of the normal acoustic impedance values. In Figure 1, such a scaling has been applied to EI (30 degrees). As stated, elastic impedance also provides a convenient way of producing synthetic seismograms for variable angles of incidence. The computed EI (30 degree) log curve can be used for producing synthetic seismograms, which could now be used for correlation with far-offset/angle stack. In Figure 2 we show the correlation of a synthetic seismogram (generated with the acoustic impedance log curve) with the near-stack from the Magdelena Valley, Colombia. The tie seems to be reasonably good. Figure 3 shows a similar synthetic seismogram (generated by using the EI log curve) tie with the far-offset stack. This tie again seems to be good – but, as expected, the amplitudes at the indicated locations on the far-stack are weaker and seem to tie accordingly with the synthetic. In Figure 4 we show a comparison of a segment of an acoustic impedance section derived from post-stack AI inversion and the equivalent EI (30 degree) section. Notice the differences in the yellow highlighted zones that enclose the gas-producing reservoir. While the hydrocarbon-bearing zone is indicated on the AI section, it appears more pronounced and convincing – and its correlation with the overlaid impedance curve also is much better than the correlation with the AI section. Thus elastic impedance attribute serves to combine the benefits of working with inverted data with far-angle data where the fluid information resides. We thank PetroNorte, Colombia, for giving us permission for presentation of the results shown in this study. We also thank Arcis Seismic Solutions for permission to present this work. |

 General statement
General statement