Figure Captions
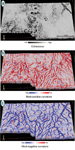
Figure 1a shows a
time-structure map at about 1850 ms, interpreted from a  3-D
3-D seismic
volume acquired in Alberta, Canada. The horizon was manually picked
across a grid of control lines to generate the horizon-based
curvature images displayed in Figures 1b and
1c. Both of these displays are contaminated by strong N-S and
E-W acquisition footprints.
seismic
volume acquired in Alberta, Canada. The horizon was manually picked
across a grid of control lines to generate the horizon-based
curvature images displayed in Figures 1b and
1c. Both of these displays are contaminated by strong N-S and
E-W acquisition footprints.
Whether due
to limitations in the survey design, coherent noise, or systematic
errors in  data
data processing, an acquisition footprint is related to
the source and receiver geometry and has little correlation to the
subsurface geology.
processing, an acquisition footprint is related to
the source and receiver geometry and has little correlation to the
subsurface geology.  Horizons
Horizons picked on noisy seismic
picked on noisy seismic  data
data contaminated with acquisition footprint, or picked through regions
where no consistent impedance contrast exists (such as channels,
turbidites, mass transport complexes, and karst), can lead to
inferior curvature measures. A significant advance in curvature
analysis has been the volumetric estimation of curvature, which
alleviates the need for
contaminated with acquisition footprint, or picked through regions
where no consistent impedance contrast exists (such as channels,
turbidites, mass transport complexes, and karst), can lead to
inferior curvature measures. A significant advance in curvature
analysis has been the volumetric estimation of curvature, which
alleviates the need for  picking
picking
 horizons
horizons in regions where no
continuous surface exists.
in regions where no
continuous surface exists.
Even when
spatial filtering is used to minimize effects of an acquisition
footprint, horizon-based curvature estimates may still suffer from
footprint artifacts. In contrast, curvature attribute values
extracted from volumetric curvature computations yield displays that
are free of artifacts and make more geologic sense.
As examples,
Figures 1d and 1e show the most-positive
and most-negative volumetric curvature attributes extracted along
the horizon surface in Figure 1a. Notice
that these displays are free of the N-S and E-W artifacts seen in
Figures 1b and 1c, and show arcuate
folds indicated by yellow arrows. The advantages of volumetric
attributes are two-fold:
1) As shown
in Figure 1, the images have a higher
signal-to-noise ratio. Volumetric estimates of curvature are
computed not from one picked  data
data sample, but rather from a vertical
window of seismic samples (in our case, 11 samples) and are
statistically less sensitive to noise.
sample, but rather from a vertical
window of seismic samples (in our case, 11 samples) and are
statistically less sensitive to noise.
2) Not
every geologic feature that we wish to interpret falls along a
horizon that can be interpreted. Often the target of interest falls
above or below a strong, easily picked horizon.
Curvature images having different
spatial wavelengths provide different perspectives of the same
geology. Tight (short-wavelength) curvature delineates small
details, such as intense, highly localized fracture systems. Broad
(long-wavelength) curvature enhances smooth, subtle flexures that
are difficult to see in conventional seismic  data
data , but which are
often correlated to fracture zones that are below seismic resolution
and to collapse features and diagenetic alterations.
, but which are
often correlated to fracture zones that are below seismic resolution
and to collapse features and diagenetic alterations.
Figure 2 shows displays of strat-cubes
near 1620 ms from coherence, most-positive (both long-wavelength and
short-wavelength) and from short-wavelength, most-negative curvature
volumes that intersect a random line that cuts across the
fault/fracture trends. The red peaks (Figures
2b and 2c) on the fault lineaments (running almost north-south)
correlate with the upthrown signature on the seismic  data
data . The
most-negative curvature strat-slice (Figure
2d) shows the downthrown edges on both sides of the faults
highlighted in blue.
. The
most-negative curvature strat-slice (Figure
2d) shows the downthrown edges on both sides of the faults
highlighted in blue.
Figure 3a
shows the horizon slice extracted from the most-positive curvature
volume at a zone of interest. There are a number of fracture
lineaments delineated by yellow picks. The density and orientations
of these lineaments have been combined into the rose diagram shown
in Figure 3b, which retains the colors
of the lineaments. This rose diagram can be compared with a similar
diagram obtained from borehole image logs to gain confidence in the
seismic-to-log calibration. Once a favorable match is obtained, the
interpretation of fault/fracture orientations and the intervals over
which they dominate can then be trusted for a more quantitative
analysis – which, in turn, is useful for optimal characterization of
reservoirs.
So far we
have demonstrated the application of the most-positive and
most-negative curvature attributes for detecting faults and
fractures and calibration with borehole image-log  data
data . Now we
illustrate the application of these attributes for mapping channels,
levees and other stratigraphic features – particularly in older
rocks that have undergone differential compaction.
. Now we
illustrate the application of these attributes for mapping channels,
levees and other stratigraphic features – particularly in older
rocks that have undergone differential compaction.
In
Figure 4 we generate strat-cube displays
through volumetric estimates of coherence, combined with
most-positive and most-negative curvatures. A strat-cube is a
sub-volume of seismic  data
data or its attributes, either bounded by two
or its attributes, either bounded by two
 horizons
horizons that may not necessarily be parallel, or spanning seismic
that may not necessarily be parallel, or spanning seismic
 data
data above and/or below a given horizon. The displayed surfaces are
4 ms below the horizon used for generating the strat-cube. Notice
the clarity with which the north-south main channel stands out and a
second channel in the top-right corner.
above and/or below a given horizon. The displayed surfaces are
4 ms below the horizon used for generating the strat-cube. Notice
the clarity with which the north-south main channel stands out and a
second channel in the top-right corner.
Because of
differential compaction and the presence of levees, the
most-positive curvature defines the flanks of the channels,
potential levees, and overbank deposits. The most-negative curvature
highlights the channel axes or thalwegs. The coherence image is
complementary and is insensitive to structural deformation of the
surface; instead, it highlights those areas of the channel flanks
where there is a lateral change in the waveform due to tuning.
In Figure 5 we show a chair display for
a strat-cube constructed from the most-positive curvature attribute
volume and an associated seismic profile. Notice how the lineaments
corresponding to the levees of the channels correlate with the
localized “highs” on the seismic section. Once an interpreter is
able to see such a convincing correlation, the interpretation of
smaller lineaments can be performed with more confidence.
In
Figure 6 we re-examine a survey
discussed in detail by Sagan and Hart in the November, 2006,
AAPG Bulletin on hydrothermally altered dolomite. In
Figure 6a and 6b, respectively, we
display time slices through the most-negative curvature volume at
approximately the Trenton and basement levels.
Note that by
using a volumetric estimate of curvature, we can map the same
diagenetically altered zones at the Trenton level and faults in the
basement discussed by Sagan and Hart (2006).
The structural control and
diagenetic alteration result in a suite of en echelon valley-like
features running northwest-southeast through the survey.
Like all
attributes, curvature is valuable only when coupled with a geologic
model of structural deformation, stratigraphic deposition, or
diagenetic alteration. Curvature is particularly sensitive to
flexures and faults. Curvature can be a powerful tool in mapping
channels, levees, bars, contourites, and other stratigraphic
features, particularly in older rocks that have undergone
differential compaction.
Discrete
fractures often appear on most-negative curvature. This behavior can
be caused by sags about the fractures or by local velocity changes
associated with stress, porosity, diagenetic alteration, or fluid
charge. Although curvature attributes calculated on time surfaces
after spatial filtering can display interesting features, volumetric
curvature attributes provide more valuable information on fracture
orientation and density in zones where seismic  horizons
horizons are not
trackable.
are not
trackable.
Reference
Sagan, J.A., and
B.S. Hart, 2006, Three-dimensional seismic-based definition of fault
related porosity development: Trenton-Black River interval, Saybrook,
Ohio: AAPG Bulletin, v. 90, p. 1763-1785.
Acknowledgment
The authors thank Arcis Corporation for permission to show the  data
data examples and publish this work
examples and publish this work
.
 Click to
view article in PDF format.
Click to
view article in PDF format. 3-D
3-D seismic
seismic  data
data volumes.
An interpreter defines surface patches of a given size, which appropriate
software algorithms then fit with a mathematical quadratic surface. Curvature
measures computed from the coefficients of this quadratic surface include:
volumes.
An interpreter defines surface patches of a given size, which appropriate
software algorithms then fit with a mathematical quadratic surface. Curvature
measures computed from the coefficients of this quadratic surface include: