Click to
view article in PDF format.
Click to
view article in PDF format.
GCMapping Geologic Features Using Seismic Curvature*
By
Satinder Chopra1 and Kurt J. Marfurt2
Search and Discovery Article #40272 (2008)
Posted February 7, 2008
*Adapted from the Geophysical Corner column, prepared by the authors, in AAPG Explorer, November, 2007, Part 1, entitled “Using Curvature to Map Faults, Fractures”, and December, 2007, Part 2, entitled “Curvature Can Be a Map to Clarity”. Editor of Geophysical Corner is Bob A. Hardage ([email protected]). Managing Editor of AAPG Explorer is Vern Stefanic; Larry Nation is Communications Director.
1Arcis Corporation, Calgary, Canada ([email protected])
2University of Oklahoma ([email protected])
General Statement
Curvature is a measure of the deviation of a surface from a plane. The more a surface is structurally flexed, folded or faulted, the larger its curvature. Curvature can indicate domes and sags associated with salt and shale diapirism, differential compaction, and diagenetic dissolution and collapse, as well as predict paleostress and areas favorable for natural fractures.
Curvature is usually
computed from picked  horizon
horizon surfaces interpreted on 3-D seismic data volumes.
An interpreter defines surface patches of a given size, which appropriate
software algorithms then fit with a mathematical quadratic surface. Curvature
measures computed from the coefficients of this quadratic surface include:
surfaces interpreted on 3-D seismic data volumes.
An interpreter defines surface patches of a given size, which appropriate
software algorithms then fit with a mathematical quadratic surface. Curvature
measures computed from the coefficients of this quadratic surface include:
1) Curvedness.
2) Azimuth of minimum curvature.
3) Shape index.
4) Minimum, maximum, most-positive, most-negative.
5) Dip.
6) Strike curvatures.
We find the most-positive and most-negative curvatures to be the easiest measure to visually correlate to features of geologic interest.
|
uFigure CaptionsuMethoduFaults and Fractures
uFigure CaptionsuMethoduFaults and Fractures
uFigure CaptionsuMethoduFaults and Fractures
uFigure CaptionsuMethoduFaults and Fractures
uFigure CaptionsuMethoduFaults and Fractures
uFigure CaptionsuMethoduFaults and Fractures
|
Method
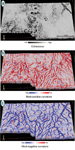
Figure 1a shows a
time-structure map at about 1850 ms, interpreted from a 3-D seismic
volume acquired in Alberta, Canada. The
Whether due
to limitations in the survey design, coherent noise, or systematic
errors in data processing, an acquisition footprint is related to
the source and receiver geometry and has little correlation to the
subsurface geology. Horizons picked on noisy seismic data
contaminated with acquisition footprint, or picked through regions
where no consistent impedance contrast exists (such as channels,
turbidites, mass transport complexes, and karst), can lead to
inferior curvature measures. A significant advance in curvature
Even when
spatial filtering is used to minimize effects of an acquisition
footprint,
Faults and Fractures
As examples,
Figures 1d and 1e show the most-positive
and most-negative volumetric curvature attributes extracted along
the 1) As shown in Figure 1, the images have a higher signal-to-noise ratio. Volumetric estimates of curvature are computed not from one picked data sample, but rather from a vertical window of seismic samples (in our case, 11 samples) and are statistically less sensitive to noise.
2) Not
every geologic feature that we wish to interpret falls along a
Curvature images having different spatial wavelengths provide different perspectives of the same geology. Tight (short-wavelength) curvature delineates small details, such as intense, highly localized fracture systems. Broad (long-wavelength) curvature enhances smooth, subtle flexures that are difficult to see in conventional seismic data, but which are often correlated to fracture zones that are below seismic resolution and to collapse features and diagenetic alterations.Figure 2 shows displays of strat-cubes near 1620 ms from coherence, most-positive (both long-wavelength and short-wavelength) and from short-wavelength, most-negative curvature volumes that intersect a random line that cuts across the fault/fracture trends. The red peaks (Figures 2b and 2c) on the fault lineaments (running almost north-south) correlate with the upthrown signature on the seismic data. The most-negative curvature strat-slice (Figure 2d) shows the downthrown edges on both sides of the faults highlighted in blue.
Figure 3a
shows the
|