![]() Click to view this article in PDF format.
Click to view this article in PDF format.
GCSeismic
Static  Corrections
Corrections *
*
By
Don W. Steeples1 and Gregory S. Baker
Search and Discovery Article #40047 (2002)
*Adapted for online presentation from
an article by the same author in AAPG Explorer (June, 1998), entitled
“Finding Seismic Static  Corrections
Corrections .” Appreciation is expressed to the author
and to M. Ray Thomasson, former Chairman of the AAPG Geophysical Integration
Committee, and Larry Nation, AAPG Communications Director, for their support of
this online version.
.” Appreciation is expressed to the author
and to M. Ray Thomasson, former Chairman of the AAPG Geophysical Integration
Committee, and Larry Nation, AAPG Communications Director, for their support of
this online version.
1University of Kansas ([email protected]).
|
|
where Dtstatic is a first-order approximation assuming the angle from vertical of h is small (ratio of V1/V0 is large).
General Statement
Static
The velocity-variation component of the
correction involves what is commonly called the "weathered zone." In
some places the weathered zone consists mostly of unconsolidated,
The primary purpose of this article is to show that when low-velocity surface layers are present, a thickness of even a few feet can have profound static effects. Introduction
Most methods used to attack the
static-correction problem depend upon using the
The problem in its most elementary form, with
a point source and a two-geophone receiver array, is depicted in Figure
1. Note that in this case the surface topography is flat, but there is a
variation in the thickness of the low-velocity material (V0)
that overlies a higher-velocity layer (V1).
When the velocity of the The first-order static correction for the geologic situation depicted in Figure 1 is shown graphically in Figure 2: The amount of static correction necessary is highly dependent on the velocity of the unconsolidated material (V0) and is not strongly dependent on the velocity of the underlying higher-velocity layer (V1). Under conditions similar to those presented in Figure 1, knowing both the velocity and the thickness of the V0 material is especially important.
Very- Many seismologists believe that P-wave velocity in earth materials is never less than about 1,100 ft/s (the velocity of sound in air). The Wyllie-equation argument says that the seismic P-wave velocity in a material is an average of the velocity in the pore fluid (air) and the mineral grains through which the seismic wave passes. This argument is used in the analysis of borehole sonic logs in water-saturated solid rock, where it usually works quite well.
In reality, the Wyllie-equation argument has
very little to do with the P-wave velocity in unconsolidated materials
because velocity is dependent only upon the shear modulus, the bulk
modulus, and the density of the total material, not on the average of
these properties for the constituent materials. The other reason that
1,100 ft/s is often quoted as a minimum velocity is that most seismic
sources emit some audible sound, called air wave, into the air. When the
velocity in the Ultra-shallow velocity measurementsFigure 3 shows four representative field files from an ultra-shallow seismic-reflection survey conducted near the Arkansas River a few miles east of Great Bend, Kan. The first reflections come from the boundaries between intra-alluvial layers at depths of two to four feet. The deepest reflection is from the water table, at a depth of about eight feet. The interval velocity varies quickly from less than 650 ft/s above the water table to more than 2,000 ft/s below it.
To obtain this degree of detail, geophone
intervals of two inches were used. The seismic source was a single,
.22-caliber rifle shot, using short ammunition, with the tip of the
rifle barrel inserted about four inches into a 3/4-inch-diameter hole in
the ground. The dominant frequency is about 450 Hz, which, when combined
with the To determine the velocities even closer to the surface, we have obtained P-wave velocity measurements with refraction surveys using an automotive spark plug as an energy source. We obtained a 100-foot-long spark-plug wire from an automotive supply company and hooked one end of the wire to the distributor of a vehicle and the other end to a spark plug placed in a hole 1/2-inch deep and 1/2-inch in diameter, located about one inch from the nearest geophone. Although it has very low power, the spark plug is a highly-repeatable, high-frequency source.
Figure 4 shows a detailed ultra-shallow field
file from a test site in Lawrence, Kansas, using the spark-plug source.
The velocity of the Discussion
In the first section, we showed the potential
effects of very-low
We believe that having accurate information about the velocity and
thickness of |

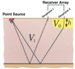 Figure 1.
Simple point-source/ receiver-array model with flat topography. The
static shift from Geophone 1 to Geophone 2 is
Figure 1.
Simple point-source/ receiver-array model with flat topography. The
static shift from Geophone 1 to Geophone 2 is Figure 2. Static correction in ms/ft for
various surface alluvial velocities (V
Figure 2. Static correction in ms/ft for
various surface alluvial velocities (V Figure 3. Four uninterpreted (top) and
interpreted (bottom) representative field files from a recent
ultra-shallow seismic-reflection survey near Great Bend, Kan. The
horizontal axis is source-to-receiver offset in feet. The source was a
single shot from a .22-caliber rifle, and the single-geophone group
interval is two inches. Digital frequency and f-k filtering has been
applied, as well as AGC scaling. The lateral distance from the shotpoint
on the left to the shotpoint on the right is 40 feet. Within that
distance, the
Figure 3. Four uninterpreted (top) and
interpreted (bottom) representative field files from a recent
ultra-shallow seismic-reflection survey near Great Bend, Kan. The
horizontal axis is source-to-receiver offset in feet. The source was a
single shot from a .22-caliber rifle, and the single-geophone group
interval is two inches. Digital frequency and f-k filtering has been
applied, as well as AGC scaling. The lateral distance from the shotpoint
on the left to the shotpoint on the right is 40 feet. Within that
distance, the  Figure 5. A 1-D solution to the three-layer
problem from the first arrivals picked in Figure 4.
Figure 5. A 1-D solution to the three-layer
problem from the first arrivals picked in Figure 4.