![]() Click to view page images in PDF format.
Click to view page images in PDF format.
UNDERSTANDING THE FRESNEL ZONE
R.E. SHERIFF*
Search and Discovery Article #40014 (2001)
Adapted for online presentation from article of the same title by the same author in Geophysical Corner, AAPG Explorer, October, 1996. Appreciation is expressed to the author and to M. Ray Thomasson, former Chairman of the AAPG Geophysical Integration Committee, and Larry Nation, AAPG Communications Director, for their support of this online version.
*University of Houston, Houston, Texas ([email protected]).
Statement of Problem
“Limit of seismic resolution” usually makes us wonder, how thin a bed can we see? Yet seismic data is subject to a horizontal as well as a vertical dimension of resolution.
The horizontal dimension of seismic resolution is described by the “Fresnel Zone.”
Huygen’s principle states that each part of a wavefront is the source of a new wave. If you’ve watched waves in a lake pass by a solid seawall jutting into the lake, you know that the waves fill in the water behind the seawall. Seismic waves behave in a similar manner when being reflected from a subsurface reflector with an anomaly on it.
The area where the waves interfere with each other constructively is our area of concern, called the “First Fresnel Zone.” The anomaly will be seen throughout this region, and this has caused dry holes to be drilled on anomalies that were off to the side of the seismic line.
List of Figures
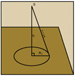 Figure 2 – The Pythagorean theorem allows one to
calculate the radius of the Fresnel Zone.
Figure 2 – The Pythagorean theorem allows one to
calculate the radius of the Fresnel Zone.
Click here for sequence of 2-D lines over 3-D model.
Fresnel Zone
The reflected waves will interfere constructively where their travel paths differ by less than a half wavelength (see Figure 1), and the portion of the reflecting surface involved in these reflections is called the First Fresnel Zone.
Beyond this First Fresnel Zone region interference will be alternatively destructive and constructive. Fresnel showed that the destructive contribution of some of these zones beyond the First Fresnel Zone will be offset by the constructive contribution of other zones – and thus the reaction of the reflector responsible for a reflection will be only that of the First Fresnel Zone.
In other words, a reflection that we think of as coming back to the surface from a point is actually being reflected from an area with the dimension of the First Fresnel Zone. The adjective “first” is often dropped.
The dimensions of the Fresnel Zone can be calculated easily by simple geometry. This is shown in Figure 2 for a plane reflector in the constant velocity case, allowing for two-way travel time.
Note that the Fresnel Zone radius depends on wavelength (itself a function of frequency and velocity). For seismic frequencies and the depths of interest to oil finders, the resulting dimensions are quite large (Figure 3).
The effect of migration can be thought of as lowering geophones through the earth until they are coincident with a reflector, at which time the Fresnel Zone will have shrunk to a small circle. If the data and migration are two-dimensional, then the Fresnel Zone will have only shrunk in one dimension and will still extend its full width perpendicular to the line (Figure 4).
Much of the improvement of 3-D over 2-D is because of this difference.
Figure 2 can be turned upside down to show the portion of the surface affected by the reflectivity at a print on the reflector (Figure 5). If we wish to preserve amplitudes so that we can interpret amplitude variations as changes in acoustic impedance, porosity, hydrocarbon accumulations, lithology, porosity-thickness, etc., we must integrate over all of the affected surface in the migration process in order to get the correct relative value.
Thus, if we are to compute porosity-thickness correctly from a 3-D seismic survey, the survey must extend for the full Fresnel-zone radius beyond the field.
Because of data coming out of the plane on the 2-D profiles shown in the model (Figure 6), the algal mound is seen on all profiles that are within a 1,000-foot window. A profile only 800 feet away looks identical to one over the center of the feature. Hence, any survey must extend beyond the area over which one intends to interpret amplitude changes by a fringe distance required by the migration process.

 Figure1 – Within a Fresnel Zone reflection
contributions arrive coherently and thus reinforce. Outside peaks and troughs
tend to cancel each other and thus make little net contribution.
Figure1 – Within a Fresnel Zone reflection
contributions arrive coherently and thus reinforce. Outside peaks and troughs
tend to cancel each other and thus make little net contribution.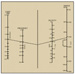 Figure 3 – Nomogram for determining Fresnel Zone
radius. A straight line connecting the two-way time and frequency intersects the
central line at the same point as a line connecting the average velocity and the
Fresnel Zone radius. For example, a 20-Hz reflection at 2.0 seconds and velocity
of 3.0 km/s has a Fresnel Zone radius of 470 m.
Figure 3 – Nomogram for determining Fresnel Zone
radius. A straight line connecting the two-way time and frequency intersects the
central line at the same point as a line connecting the average velocity and the
Fresnel Zone radius. For example, a 20-Hz reflection at 2.0 seconds and velocity
of 3.0 km/s has a Fresnel Zone radius of 470 m.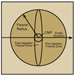 Figure 4 – Three-dimensional migration collapses
the Fresnel Zone to a small circle, but 2-D migration collapses it in only one
direction.
Figure 4 – Three-dimensional migration collapses
the Fresnel Zone to a small circle, but 2-D migration collapses it in only one
direction.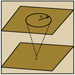 Figure 5 – A given point on a reflector affects a
surface region by an area equal to the Fresnel Zone. In migration the entire
Fresnel Zone must therefore be summed over to obtain the correct amplitude.
Figure 5 – A given point on a reflector affects a
surface region by an area equal to the Fresnel Zone. In migration the entire
Fresnel Zone must therefore be summed over to obtain the correct amplitude. Figure 6 – Model demonstrating out-of-the-plane
imaging and Fresnel Zone effects on data over a hypothetical reef with the
specified offsets. The false image in this example is clearly seen 1,500 feet
away (after Waldo Jackson and Fred Hilterman).
Figure 6 – Model demonstrating out-of-the-plane
imaging and Fresnel Zone effects on data over a hypothetical reef with the
specified offsets. The false image in this example is clearly seen 1,500 feet
away (after Waldo Jackson and Fred Hilterman).