|
Figure Captions
 Figure
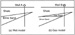
1. Two geological models that will illustrate the basics of the  AVO
method.
 Figure
2. A simple drawing of P- and S-wave motion.
 Figure
3. The velocities, densities and synthetic seismograms for model A.
 Figure
4. The velocities, densities and synthetic seismograms for model B.
 Figure
5. A stacked section from Alberta showing a "bright-spot" at
640 msec caused by a Cretaceous gas sand.
 Figure
6. The geometry of a reflected P-wave at a given angle a. The offset is
the distance from the source to the receiver.
 Figure
7. The CDP gathers from a portion of the stacked section in Figure 6,
over the "bright-spot". Notice the amplitude increase
indicated at the zone shown by an arrow.
 Figure
8. The intercept and gradient fit to the top and base reflections from a
gas sand.
 Figure
9. The intercept (a) and gradient (b) for the example shown in Figures
6
and 7.
 Figure
10. The sum (a) and difference (b) of the intercept and gradient shown
in Figure 9.
 Figure
11. A 3D AVO example from a Cretaceous channel sand in Alberta. The plot
shows the sum of intercept and gradient, or pseudo-Poisson's ratio.
Return
to top.
AVO, which stands for Amplitude Variations
with Offset--or, more simply, Amplitude Versus Offset--is a seismic
technique that looks for direct hydrocarbon indicators using the
amplitudes of prestack seismic data. The basics of the AVO method will
be explained here using the two geological models shown in
Figure
1:
Wells
have been drilled into each sand.
P- and S Waves
To
understand the AVO effects of these two models, we must first discuss
seismic waves and the recording of seismic data. Traditional seismic
data are recorded using compressional waves, or P-waves, which move
through the earth by alternately, compressing and expanding the rocks in
their direction of propagation. However, there is a second type of wave
called a shear wave, or S-wave, which travels by shearing the rocks at
right angles to its direction of propagation. This is illustrated in
Figure 2.
There
are several important differences between P- and S-waves:
-
First,
the velocity of the S-wave is slower than the velocity of the P-wave
for a given geological formation.
-
Second,
S-waves are less sensitive to the presence of gas in a reservoir
than P-waves. since the high compressibility of gas has more of an
effect on the Pwave velocity.
-
A
third important physical parameter is the density that is strongly
affected by the presence of gas.
Figures
3 and 4 show the P-wave velocity, S-wave velocity and density logs for
the two models of Figure 1. Notice that both the P-wave velocity and the
density are lower in the gas sand than in the wet sand, but the S-wave
velocity is the same in both cases. To understand how this is related to
the recorded seismic trace, note that the seismic recording measures two
things: the time that it takes to travel down to a particular geological
interface, and the reflection amplitude.
Figures
3 and 4
also show how the amplitudes are created. First, we multiply the
velocity times the density to get the P or S impedance. Then, we
calculate the difference between the impedances divided by their sum,
which gives us a reflection coefficient (reflectivity) at each
interface. Finally, we superimpose the seismic response, or wavelet, on
the reflection coefficients to get the synthetic seismic traces shown at
the far right of both figures.
The
P and S synthetics for the wet model are almost identical, but for the
gas model the S-wave synthetic is the reverse of the P-wave synthetic
and has lower amplitudes. The high amplitude reflections seen on the
P-wave response of the gas model are called "bright-spots,"
and can be effective in the Gulf Coast and other areas in the search for
gas sands. Figure 5 shows such a bright-spot reflection from a shallow
Cretaceous play in Alberta at 640 msec.
However,
there are other geological situations that create 'bright-spots,"
such as coal seams or hard streaks. From this discussion, it is obvious
that the P-wave response does not reveal the presence of gas
unambiguously, and it needs to be supplemented with an S-wave recording.
Unfortunately, S-wave recording is not that common. This leads us to the
AVO method, which allows us to derive a similar result without actually
recording an S-wave section.
Return
to top.
The
AVO Method
Figure
6, which shows a typical prestack seismic raypath, records that the
incident wave displays both compressional and shear effects, since it
strikes the interface at an angle a. The reflected wave thus contains
the effects of both P- and S-waves. Although the mathematics of this
process has been known since the nineteenth century, it was only very
recently that we have recognized it on our seismic data. Ostrander
(1984) showed that, for the simple model of
Figure
1b, the amplitudes on
a prestack gather would increase with offset. This is shown in
Figure
7,
in which the reflections from the gathers (seismic traces from one point
displayed side by side) over the shallow gas sand of
Figure 6 are seen
quite clearly to increase.
Not
all gas sands show increasing AVO effects, since the result is dependent
on the nature of the acoustic impedance change. The different types of
AVO anomalies have been classified as classes 1, 2 and 3 by Rutherford
and Williams (1989} In the present paper we are looking at a Class 3
example, in which the impedance of the sand is lower than the encasing
shale.
If
we measure the amplitude of each reflection amplitude as a function of
offset, and plot them on a graph as a function of the sine of angle of
incidence squared, we observe a straight line. For any line, the
intercept and gradient can be measured. By linearizing the complicated
mathematics behind the AVO technique, Richards and Frasier (1976) and
Wiggins et al. (1986) gave us the following physical interpretation of
the intercept and gradient:
Intercept = the P-wave reflection amplitude.
Gradient = the P-wave reflection amplitude minus
twice the S-wave reflection amplitude.
To
illustrate this point, the amplitudes from a small portion of one of the
gathers in Figure 7 are shown in
Figure
8, with a straight line fit
superimposed. Notice that the top of the sand has a negative intercept
(a trough) and a negative gradient, and the base of the sand has a
positive intercept (peak) and a positive gradient. When we perform this
analysis at every sample, on every gather, we create two sections, or
volumes. The intercept section is similar to the conventional
stack--except that it represents a better estimate of the vertical
P-wave reflections. The gradient contains information about both the P
and S-wave reflections.
There
are many ways of displaying this information. As well as displaying the
intercept and gradient on their own, it is common to display the
difference and sum of the intercept and gradient. From the above
explanation it is obvious that the difference, after scaling, is the
approximate S-wave reflectivity. The sum of the intercept and the
gradient can be shown to represent the approximate Poisson's ratio
change, where Poisson's ratio is related to the square of the P-wave to
S-wave velocity ratio. A negative Poisson's ratio change is associated
with the top of a gas zone, whereas a positive change is associated with
the base.
These
displays are shown in Figures 9 and
10 for our real example. Notice that
the intercept (P-wave) shows a strong "bright-spot," whereas
the pseudo-S-wave (intercept minus gradient) does not show a
"bright-spot," indicating the presence of a gas sand.
As
one final example, let us consider an example of the AVO technique
applied to 3-D data. Figure 11 shows the sum of intercept and gradient,
or pseudo-Poisson's ratio computed over the top of a channel sand in
Alberta. The negative values on this plot indicate the possible presence
of gas in the channel sand.
Conclusion
This
tutorial has reviewed the basic principles behind the AVO technique. We
have concentrated on a single type of anomaly, the Class 3, in which the
acoustic impedance of the gas sand drops with respect to the encasing
shales. For a discussion of other types of anomalies refer to the papers
by Rutherford and Williams (1989), Ross and Kinman (1995). and Verm and
Hilterman (1995).
The
key thing to remember about the AVO method is that the AVO gradient
responds to both P- and S-wave reflections from an interface, and this
behavior can be used to locate gas charged reservoirs. Applied to 3-D
seismic data, the AVO technique gives us a robust and inexpensive method
for identifying potential reservoirs and is a technique that adds an
extra dimension to studies done only with stacked seismic data.
Ostrander,
W.J., 1984, Plane-wave reflection coefficients for gas sands at
nonnormal angles of incidence: Geophysics, v. 49, p. 1637-1648.
Richards, P.G., and Frasier, C.W., 1976, Scattering of
eleastic waves from depth-dependent inhomogeneities: Geophysics, v. 41,
p. 441-458.
Ross, C.P., and Kinman, D.L., 1995, Nonbright-spot AVO;
two examples: Geophysics, v. 60, p. 1398-1408.
Rutherford, S.R., and Williams, R.H., 1989,
Amplitude-versus-offset variations in gas sands: Geophysics, v. 54, p.
680-688.
Verm, R., and Hilterman, F., 1995, Lithology, color-coded
siesmic sections; the calibration of AVO crossplotting to rock
properties: Leading Edge, v. 14, p. 847-853.
Wiggins, W.,
Ng, P., and Manzur, A., 1986, The relation between the VSP-CDP
transformation and VSP migration
(abstract): SEG Abstracts, v. 1, p. 565-568.
Return
to top.
|
Print this page
Click to view this article in PDF format.