|
The biggest distinction between geology and geophysics can probably be
broken down into the different domains from which they both start their
work. The geologist works in terms of spatial coordinates and depth,
with perhaps the roadcut epitomizing the best example of his world view.
Depth is also how he makes use of his interpretation results, i.e. a
well is drilled to a certain depth.
The geophysicist, however, deals with information recorded in time. His
job in seismic processing is to transform this information in time into
depth for the geologist to make his maps and calculate where to drill.
The geophysicist works in time because of the nature of seismic
exploration. A source is initiated at some location and sensors record
the subsequent reflections as a function of time.
Figure Captions
 Figure
1a. Determination of the depth of a water well by translating time into
distance.
Figure 1b. Complications of translating time
into distance where the well is not vertical.
 Figure
2: The velocity  field is a constant value on the top (2a), but more
complicated on the bottom (2b). The
velocity contrast on the top causes the seismic energy to bend across
the interface - and this ray bending makes the conversion to a spatially
correct depth image more complicated.
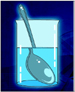 Figure
3: A simple example of light rays bending across the air-water surface.
 Figure
4: The oil trap on the left is imaged without seismic energy needing to
penetrate the salt body. The oil trap on the right is below salt, which
causes seismic energy to bend as it travels through the salt-sediment
interface. Why does this matter? Because not correcting for this ray
bending in imaging may cause the misplacement of the oil trap.
 Figure
5: The depth migration velocity field (left) looks more like the geology
the seismic data is trying to image; the result is accurate positioning
of the subsurface point (red dot). Time migration velocity field (right)
is an approximation that does not allow lateral velocity changes, making
the algorithm faster but less accurate - and the positioning of the
subsurface point is in the wrong spot (brown dot).
Return
to top.
The problem is not unlike the scenario depicted in
Figure 1a: Here we have a person
determining the depth of his water well by dropping a rock into it and
recording the time for the splashing sound to come back. After some
mathematical manipulation - and knowing the speed of sound in air - the
person can translate time into depth. This sounds simple enough, but we
made assumptions about the rock traveling straight down and the sound
traveling straight back up to our ears. If the well is not vertically
straight but deviated (Figure 1b), then
we have a more complicated problem to solve.
This is the nature of seismic exploration: We record the strength of
seismic reflections, and we can assume they all come from directly below
the surface, but more likely the reflections come from anywhere in some
three dimensional subsurface location around our surface position.
Figure 2a shows more clearly the issue.
Reflected energy from a subsurface point will travel to our surface
receivers in a straight line if the velocity field is constant. It would
be a simple and straightforward process to compute the location of the
subsurface point if we knew this velocity field. However, the issue
becomes more complicated when we acknowledge that seismic energy bends
according to Snell’s law when the velocity changes in the subsurface as
shown in Figure 2b. Obviously, there is a
lot of velocity contrast in complex geologic regimes.
Implications of Ray Bending
This ray bending is not unlike light bending as it travels through water
and air as depicted in Figure 3. The
resultant bent rays can lead to a gross misinterpretation of what is in
the glass if we do not account for it. That is the goal of seismic
imaging; accounting for the complicated velocities in the subsurface
that will distort our interpretation, especially in terms of where
features are actually located.
Figure 4 shows this distortion due to
velocity contrasts quite clearly. In both cases we are looking for the
oil trap depicted by the black shape. In one case, on the left in
Figure 4, we need only deal with the
relatively minor velocity contrast between the water column and the
subsurface when imaging the seismic reflections. In the second case, in
Figure 4 (right), the oil trap is located
below salt, so the seismic reflections will be bent sharply as they
travel through the salt body. Snell’s law tells us we will have more
ray bending with more velocity contrast. Salt
normally has a 2:1 velocity contrast with surrounding sediments, which
amounts to a great deal of ray bending. If we do not honor this ray
bending, we could spatially mislocate the oil trap as depicted by the
gray shape to the left of the actual location of the oil trap in
Figure 4
(right).
Specification of
Velocity field
One of the means we have for controlling the
processing of seismic data and the eventual placement of events comes
from the specification of a velocity field. We normally use the timing
of seismic reflections as a function of spatial position and offset to
determine this velocity field. However, we can make approximations to
the velocity field when it comes to imaging the seismic data.
There are two broad classes of imaging
algorithms available to the geophysicist. One class has historically
been referred to as time migration, while the other class has been
referred to as depth migration. The names are confusing because of the
implication as to the domain the final images are in. However, it is
possible to convert seismic data from time to depth with simple vertical
shifts of the data. The main difference in the algorithms comes about in
how they approximate the velocity field.
Time migration velocity fields will not honor
lateral velocity changes, although they can pick up vertical changes, as
depicted in Figure 5 (right). Time
migration algorithms do this for the sake of faster computation speed
and less image sensitivity to the velocity model. Depth migration
velocity fields look more like the geology you are trying to image, as
depicted in Figure 5 (left). Notice how
the velocity wedge is accurately portrayed, while the time migration
velocity field, Figure 5 (right), is a
laterally averaged representation.
The
price for the accuracy, however, is more expense - and there is a
greater need to determine the velocity field accurately. Imaging
algorithms are available, as are mechanisms to build the velocity model
Return
to top.
|
Print this page
Click to view article in PDF format.