Click to view page images in PDF format

GAS HYDRATE DISSOCIATION AND EXCESS PORE PRESSURE IN MARINE SEDIMENT

Wenyue Xu
School of Earth and Atmospheric Sciences, Georgia Institute of Technology, Atlanta, GA 30332

Introduction

It has long been suggested that gas hydrate dissociation in marine sediment may lead to excess pore pressure, which may be related to sediment failure and enhanced transport of greenhouse gas into the ocean and the atmosphere. On the other hand, a clear and adequate quantification of this excess pore pressure has not been accomplished. This investigation addresses the problem by first quantifying the volume expansion associated with gas hydrate dissociation. The volume expansion is then related either to the increased fluid pressure that drives an enhanced upward fluid flow through the overlain sediment, or to a large increase in pore pressure in cases of dissociating gas hydrates in confined pore spaces. The cases of a horizontal plane of heating or inhibitor injection are further analyzed. Finally, implications of excess pore pressure caused by gas hydrate dissociation to marine sediment deformation or failure are discussed.

Volume expansion due to gas hydrate dissociation

Gas hydrate dissociation may occur within a gas-liquid-hydrate three-phase coexistence zone of dynamically evolving natural gas hydrate systems in a rapidly changing environment. The associated total volume change dV, which includes contributions from liquid water dVw, free gas dVg and gas hydrate dVh, resulting from the dissociation of dVh gas hydrates is

                    (1)

where the factor of volume expansion

                        (2)

where r_g is the mass fraction of gas in the gas hydrate, and _w, _g and _h denote the densities of liquid water, free gas and gas hydrate, respectively. Rv is affected mostly by the change in gas density, which is usually highly compressible and is less affected by temperature. Dissociation of gas hydrate leads to volume expansion when Rv>0, whereas a volume contraction will result if Rv<0. Calculations indicate that, for pure water or normal seawater, Rv decreases with pore pressure from ~5 at ~7.5 MPa to 1 at 12 MPa and to ~0.3 at ~34 MPa.

Gas hydrate dissociation and resultant excess pore pressure

In a vertical one-dimensional system, neglecting the initially small amount of free gas, the volume increase resulting from the dissociating gas hydrates is mostly accounted for by an increase in the rate of upward fluid flow above the gas hydrate dissociation zone

                                            (3)

where f is the fluid density, and V and Vh are volumes per unit section area of the vertical column. This increase in the flow rate can be directly related to a corresponding increase of pressure gradient according to Darcy’s law

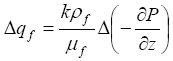                                                            (4)

where k denotes the permeability of sediment and mf is the fluid viscosity. The increase in pressure gradient may be approximated as

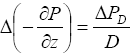                                                                        (5)

where P_D is the pressure increase at a depth D below the seafloor but above the dissociation area. Combining equations (3), (4) and (5) yields

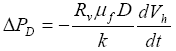                                                            (6)

Equations (6) indicates that the magnitude of excess pore pressure P_D resulting from gas hydrate dissociation is proportional to the factor of volume increase Rv, the rate of dissociation dVh/dt and the depth below seafloor D, and inversely proportional to the permeability k. Figure 1 plots the excess pore pressure P_D, at D=40 meters below the seafloor, as a function of the seafloor depth and the rate of dissociation dVh/dt calculated for k=10^-16 m² and µf=10^-4 kg/m/sec. The calculation is consistent with the result of an earlier numerical modeling of the response of a marine gas hydrate system to a temperature increase at seafloor.

Excess pore pressure caused by heating

Heating is one of the primary methods that have been proposed for extracting natural gas from natural gas hydrate reservoirs. For simplicity, here we consider a horizontal heating plane within or immediately below a gas hydrate layer such that the whole system can be viewed vertically as one-dimensional. Assume a heating rate of Qe, which is provided to dissociate gas hydrates while heat up the hydrate-bearing sediment within and near the dissociation area, namely

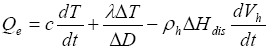                                           (7)

where H_dis is the heat of gas hydrate dissociation, is the effective thermal conductivity, and c is the effective heat capacity consisting of contributions from the individual phases and the host sediment, averaged across the dissociation zone D:

        (8)

where s  and Cs are the density and the specific heat, respectively, of the sediment host, and _h, c_h, S_h, _g, c_g, Sg, and _l, c_l and S_l are the density, the specific heat and the volume fraction of gas hydrate, free gas and liquid solution, respectively. For simplicity, assuming thermodynamic equilibrium and neglecting the change in salinity, temperature T is a function of pore pressure within the hydrate dissociation area. Therefore,

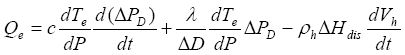            (9)

Using equation (6) the solution of equation (9) is obtained as

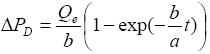                                                            (10a)

where

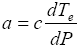                                                                                            (10b)

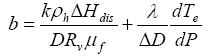                                                            (10c)

Excess pore pressure caused by inhibitor injection

Gas hydrate inhibition is another method proposed for introducing gas hydrate dissociation via injection of alcohols or glycols to lower the stability of gas hydrate. Assuming the whole process is not far away from thermodynamic equilibrium, except for during a short initial stage, the new temperature is

T=T₀+T_e                                                                                                                                (11)

where T_e is the difference between the new stability temperature T_e, corresponding to the decreasing pressure Pe, and the initial temperature T₀. On the other hand, the temperature decrease of the hydrate dissociation area leads to an additional heating from outside of the dissociation area. This heating is approximately

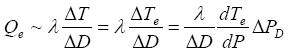                                            (12)

Similar to equation (7), the conservation of heat is described by

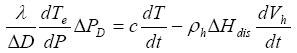                                            (13)

The solution of equation (13), obtained in a way similar to the heating case, is

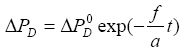                                                                        (14a)

where

                                                                (14b)

and is the maximum pressure increase, which is approximately

                                                                                    (14c)

where P₀ is the initial pore pressure before the injection and is the hydrate stability pressure shortly after the injection, which can be quite close to the equilibrium pressure at the initial temperature before the injection.

Excess pore pressure in confined pore spaces

In sediments of the real world often pore spaces can be more or less confined with respect to a rapid gas hydrate dissociation. To derive a relationship between gas hydrate dissociation and the resultant increase in pore pressure, the volume change of pre-existing free gas needs to be included in addition to that described by equation (1) in the earlier analyses. This additional volume change is found to be

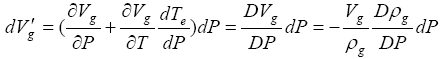               (15)

Because the total volume cannot be changed in a confined pore space, the sum of the volume changes of individual phases plus the volume change of pre-existing free gas must be zero, that is

                                        (16)

Dividing by the total volume of the pore space and using equation (15), a relationship between the changes in volume fraction of dissociated gas hydrate S_h and the magnitude of excess pore pressure P can be obtained from equation (16), which is

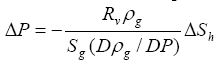                                                                            (17)

where S_g is the volume fraction of free gas in the pore space. Equation (17) does not apply to S_g<<0.01 because the compressibility of liquid solution or gas hydrates, which is much smaller than that of free gas, is neglected. When these additional volume changes are considered in the same way as for free gas, equation (17) becomes

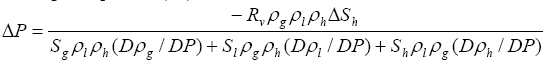  (18)

The excess pore pressure, as calculated using equation (17), is plotted as a function of pressure and S_h/S_g in Figure 2.

Implications to sediment deformation or failure

There are a few types of sediment deformation or failure that may be related to the development of excess pore pressure resulting from gas hydrate dissociation. It is found that the excess pore pressure in well-connected pores is most easily to facilitate, instead of trigger, submarine landslides involving a layer of surface sediment up to ~100 m thick in a shallow water environment of less than 1000 m water depth. On the other hand, besides its ability in causing shallow landslides, the excess pore pressure in confined pore spaces may lead to the failure of a relatively thick sediment layer in deeper water environments of 2000 m to 5000 m water depths. It is suggested that dissociation of gas hydrates residing in individual pore spaces not only has the ability to cause a partial liquefaction of the host sediment but can also produce an inter-pore shear stress, which may lead to a complete liquefaction and failure of the sediment. The same excess pore pressure may cause vertical hydraulic fractures. Together with the gravitational instability of the intensely disturbed sediment layer, this may explain the occurrence of vertical pathways of fluid flow, pockmarks and mud volcanoes associated with marine gas hydrate systems.

Figure 1.

Figure 2.