![]() Click to view article in PDF format.
Click to view article in PDF format.
GCReflector Convergence and  Rotation
Rotation Attributes Facilitate Seismic Stratigraphy Interpretation*
Attributes Facilitate Seismic Stratigraphy Interpretation*
Satinder Chopra1 and Kurt J. Marfurt2
Search and Discovery Article #40876 (2012)
Posted January 30, 2012
*Adapted from the Geophysical Corner column, prepared by the authors, in AAPG Explorer, January, 2012, and entitled “The Final Touch: Attributes Prove Their Worth”. Editor of Geophysical Corner is Bob A. Hardage ([email protected]). Managing Editor of AAPG Explorer is Vern Stefanic; Larry Nation is Communications Director.
1 Arcis Corp., Calgary, Canada ([email protected])
2 University of Oklahoma, Norman, Oklahoma
Seismic stratigraphy requires interpreters to analyze the geometrical configurations and termination patterns of seismic reflection events. Maps of distinct families of these reflection behaviors usually can be interpreted to determine where distinct depositional processes occur across the mapped area. Reflection patterns such as toplap, onlap, downlap and erosional truncation are used as architectural elements to reconstruct the depositional environments imaged by seismic data.
Using such seismic-depositional environment maps – together with well control and modern and paleo analogues – allows interpreters to produce probability maps of “most-likely” lithofacies. Although coherence and curvature are excellent for delineating some seismic stratigraphic features, they have limited value in imaging classic seismic stratigraphy features such as onlap, progradation and erosional truncation.
Here we examine how newer volumetric attributes facilitate seismic stratigraphic analysis of large 3-D seismic volumes.
|
|
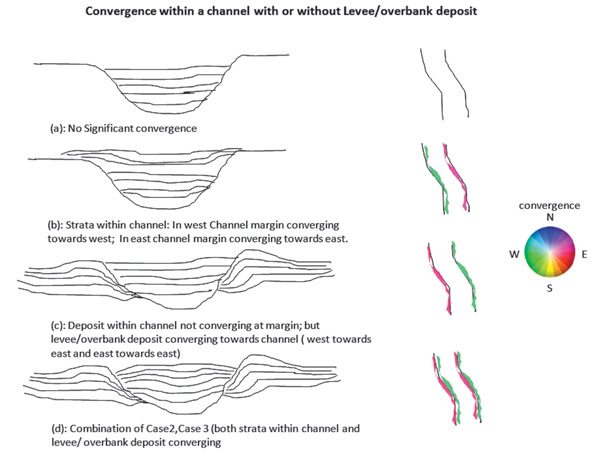
Changes in reflector dip, reflection terminations, erosional unconformities and angular unconformities are relatively easy to recognize by visual inspection of vertical seismic sections. To translate visual recognition of these features to a numerical-recognition process, a first step is to compute volumetric estimates of vector dip at each data sample. Next, the mean and standard deviations of these vector dips are calculated in small windows about each data sample. Conformable reflections will have small standard deviations of their reflection dips, while non-parallel events such as angular unconformities will have high standard deviation. In 2000, Barnes computed a vertical derivative of apparent dip along a user-defined azimuth, and used that calculation to define whether reflections diverged or converged. In this methodology, converging reflections show a decreasing change in dip while divergent reflections show increasing change in dip. Marfurt and Rich (2010) built upon this method and generated 3-D estimates of reflector-convergence azimuths and magnitudes. In order to represent the vector nature of reflector convergence in different azimuthal directions, they employed a 2-D color wheel to indicate reflector dip and azimuth. Reflection Compressive deformation and wrench faulting cause fault blocks to rotate. The extent of Fault-block In Figure 1, we show the behavior of reflection convergence for a channel with and without levee/overbank deposits for four scenarios:
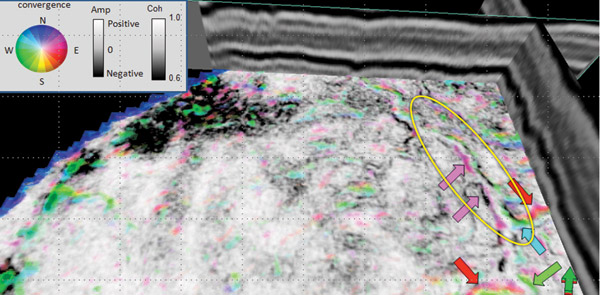
We carried out the computation of both reflector convergence and reflection Using the scenarios presented in Figure 1, our interpretation of the zone within the yellow dotted ellipse is that levee/overbank deposits converge toward the channel margin to the northeast (magenta) and southwest (green). In Figure 3 we show a time slice through a reflector- Application of two attributes, namely reflector convergence and reflector Reflector convergence measures the magnitude and direction of thickening and thinning of reflections. Reflector We thank Arcis Corporation for permission to show the data examples, as well as for the permission to publish this work. Barnes, A.E., 2000, Weighted average seismic attributes: Geophysics, v. 65/1, p. 275-285. Marfurt, K.J., and J. Rich, 2010, Beyond curvature-volumetric estimates of reflector |

 General statement
General statement