![]() Click to view article in PDF format.
Click to view article in PDF format.
Oil Shales: Their Shear Story*
Jyoti Behura1, Michael L. Batzle1, Ronny Hofmann2 and John Dorgan1
Search and Discovery Article #40379 (2009)
Posted March 16, 2009
*Adapted from oral presentation at AAPG Annual Convention, San Antonio, TX, April 20-23, 2008
1Geophysics, Colorado School of Mines, Golden, CO.
2Shell International Exploration and Production, Houston, TX. ([email protected])
Organic-rich shales house large untapped amounts of hydrocarbons. In-situ recovery of these hydrocarbons involves thermal cracking and steamflooding of these reservoirs which changes its physical properties, and shear properties in particular. We measure, within the seismic band, the complex shear modulus (and thus also the attenuation) of two oil shale samples, one rich in organic content and the other low in organic content.
Both the kerogen-rich and the lean shale show a weak dependence of modulus and  Q
Q on frequency. Their properties can be effectively considered frequency independent within the seismic band. These shales, however, show a dramatic change in shear-wave velocity and attenuation with temperature. Their shear moduli and
on frequency. Their properties can be effectively considered frequency independent within the seismic band. These shales, however, show a dramatic change in shear-wave velocity and attenuation with temperature. Their shear moduli and  Q
Q decrease with melting of the kerogen, but with the subsequent loss of some of the kerogen, both shear moduli and
decrease with melting of the kerogen, but with the subsequent loss of some of the kerogen, both shear moduli and  Q
Q increase. The magnitudes of these changes along the direction of the bedding and perpendicular to the bedding differ, which makes velocity anisotropy and attenuation anisotropy potentially valuable attributes. The velocity anisotropy and attenuation anisotropy of the shales can change significantly with temperature, in some cases by more than an order of magnitude. The amount of kerogen content in a shale also influences the velocity and attenuation. The more the organic content, the lower is the shear modulus and the higher is the attenuation.
increase. The magnitudes of these changes along the direction of the bedding and perpendicular to the bedding differ, which makes velocity anisotropy and attenuation anisotropy potentially valuable attributes. The velocity anisotropy and attenuation anisotropy of the shales can change significantly with temperature, in some cases by more than an order of magnitude. The amount of kerogen content in a shale also influences the velocity and attenuation. The more the organic content, the lower is the shear modulus and the higher is the attenuation.
|
|
Introduction
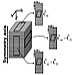
A vast unexploited source of hydrocarbons is oil shales, i.e., shales rich in kerogen. The Schlumberger Oilfield Glossary defines kerogen as "the naturally occurring, solid, insoluble organic matter that occurs in source rocks and can yield oil upon heating." The US Office of Naval Petroleum and Oil Shale Reserves estimates there are some 1.6 trillion barrels of oil contained in oil shales around the world, with 60-70% of reserves (1.0-1.2 trillion barrels) in the United States. Technical challenges and environmental concerns, however, hinder their exploitation. Environmental considerations, for example, have rendered surface-mining unfeasible. This calls for in-situ recovery, which poses new technical challenges. The most promising in-situ project is being carried out by Shell Oil Company under the name of the Mahogany Research Project in Colorado, which uses electrical heating. A heating element is lowered into the well and allowed to heat the kerogen over time, slowly converting it into oils and gases, which are then pumped to the surface. Seismic techniques can play an important role in monitoring changes in these oil shale reservoirs. Heating and steamflooding will change physical properties such as modulus, anisotropy, and attenuation, which can have a substantial effect on seismic wave propagation. The response of oil shales under varying temperature and pressure to seismic waves, however, is not well understood. To address this problem, we study the shear behavior of oil shales in the seismic frequency band by conducting torsional experiments under varying temperature and frequency. Measurements are carried out using a shear rheometer. The rock sample is clamped at both ends, and measurements are conducted with the sample dry and under no lateral confining stress. A sinusoidal torsional strain is applied on one end, and the resulting stress is recorded on the other end, which is fixed. The experiment is schematically shown in Figure 1. When a viscoelastic material is subjected to a sinusoidally varying strain, a steady state will be reached when the resulting stress is also sinusoidal, with the same angular frequency, but with a phase lag of δ, which is a measure of attenuation of that body (O'Connell and Budiansky, 1978). For an elastic material, δ=0, and for a viscous fluid, δ can approach π/2, while δ for a viscoelastic body has a value between these two limits. Note that the minimum value for The in-phase part of the stress, σ', gives the "real" or the "storage" modulus, G', and the out-of-phase part of the stress gives the "imaginary" or "loss" modulus, G", G' = σ'/ε, .........(1) G" = σ"/ε. .........(2) The
where W is the maximum elastic stored energy during a cycle of loading at the frequency under consideration and W is the energy dissipated per cycle. We analyzed two samples of shale from the same formation (Green River Formation, Colorado) with different amounts of organic content, one with ≈30% and the other with ≈5% organic content. We also examined the influence on shear wave velocity anisotropy and attenuation anisotropy. The anisotropy studies were conducted by using samples cut along three orthogonal planes (Figure 2). A sample cut parallel to the symmetry axis is used to measure the complex stiffness Č44=Č55 (Figure 2). As the shale is assumed to be transversely isotropic (TI), a sample cut in the vertical symmetry plane with its long axis orthogonal to the symmetry axis (Figure 2) would give Č44=Č55 as well. In fact, two kerogen-rich samples contained in the vertical symmetry plane, one oriented along the symmetry axis and the other perpendicular to it, gave strikingly similar results for the whole range of temperatures and frequencies studied. This supports our assumption that the shales are very likely TI. A sample cut in the isotropy plane, as shown in Figure 2, is used to obtain Č66. Dynamic mechanical analysis of the shales was carried out for temperatures ranging from 30°C to 350°C at 20°C increments, with the frequency varying from 0.01 to 80 Hz in increments of 0.1 on the log10 scale. All the measurements are carried out in the linear viscoelastic regime, at a constant strain of 8x10-5, under a variable applied axial stress which does not allow the sample to expand vertically. This is similar to reservoir recovery conditions where the shale is heated but its expansion is restricted. Figures 3a-b show the real part, C'55, and inverse Both moduli (C'55 and C'66) and attenuation (1/Q55 and 1/Q66) show a marked change with temperature. Figure 4 shows a comparison of the moduli and It is especially convenient to analyze the above changes in terms of the anisotropy parameters γ and γ γ As mentioned above, the magnitude of the effect of melting and evaporation of kerogen on C'55 and C'66 is different. This translates to a significant change in γ as seen in Figure 4a. As the kerogen melts, C'55 drops significantly compared to C'66, resulting in a jump in γ. With further increase in temperature, kerogen starts evaporating, which results in a drop in γ as the shale becomes less compliant. As with velocity anisotropy, attenuation anisotropy also shows a large change with temperature (γ γ and γ This experiment also shows the contribution of layering to the anisotropy of TI media. Bakulin (2003) has shown that the effect of layering on VTI anisotropy is of second order compared to that of intrinsic anisotropy, but if the contrast in moduli between the different layers is large, the layer-induced anisotropy can be significant. At room temperatures, the kerogen is solid and so the contrast in shear modulus of the solid clay (and carbonate) layers and the kerogen layers is not significant. This results in a low value of γ at room temperatures (Figure 5a). With increase in temperature, the kerogen progressively melts, thereby increasing the contrast between the layers. This results in a notable increase in γ caused by layering. C'55 for the lean shale under confining axial stress is shown in Figure 6a. The general trends for lean shale are similar to those for the kerogen-rich shale. The magnitudes of lean-shale moduli, however, are larger than those of the organic-rich shales because the larger clay content in the lean shale increases its modulus. This might be used as a distinguishing factor between lean and kerogen-rich shales. Velocity dispersion is weak (Figures 6a), especially within the seismic band. Attenuation is also weakly dependent on frequency. This weak frequency dependence at intermediate temperatures (around 150°C) of attenuation implies that friction may be the dominant attenuation mechanism. Later, we will give more evidence in favor of frictional attenuation. Additional experiments, however, are necessary to find out if other mechanisms, such as "squirt flow" of fluids and viscous relaxation, are playing important roles. With increase in temperature, till about 200°C, C'55 drops more rapidly than does C'66. This fall in the storage moduli is most probably due to the liquefaction of the small amount of kerogen sandwiched between the clay layers. As discussed earlier in the previous section, any change to the kerogen would influence Č55 much more than Č66, which explains the greater drop in C'55. Below 200°C, the liquefaction of kerogen not only softens the rock, bringing down C'55, but also decreases the To test if friction is the dominant loss mechanism, we conducted another set of measurements to find C'55 under constant axial stress, results for which are shown in Figure 6b. If friction were indeed the dominant loss mechanism, two major changes would occur. First, C'55 would decrease in general. Second, for temperatures above 200°C, just as when the kerogen is lost, C'55 under constant axial stress would continue to decrease. This is because under constant axial stress, after loss of some kerogen, the voids left behind are retained, which decreases C'55 further. In contrast, under increasing axial stress, the voids are occupied by the expanding clay minerals as the rock is not allowed to expand. Both these effects can be seen by comparing Figures 6a and 6b, which support friction as the dominant attenuation mechanism. In-situ recovery of oil from oil shales involves thermal processes which melt the kerogen. These changes, therefore, should have a more pronounced effect on the shear-wave properties of the shales than the P-wave properties. So a study of the shear properties of these rocks is more attractive than the study of their bulk properties and thus makes acquisition of multicomponent seismic data all the more important. Our shear property measurements, as a function of temperature, should be representative of the conditions encountered during in-situ thermal cracking and steamflooding of oil shale reservoirs. Moreover, as our measurements encompass the seismic band, they should be more representative of the seismic properties of oil shales in the field. The strong temperature dependence of the mechanical properties of oil shales makes 4D-9C seismic analysis promising. The melting of kerogen can bring down the shear velocity significantly, by as high as five times in some cases. Their Oil shales have an additional property to be exploited - anisotropy. The temperature influence on C'55 and C'66 differs, making anisotropy an important attribute. The large changes in anisotropy observed by us could be visible in seismic data. For example, there should be a notable change in the nonhyperbolic moveout of SS-waves. Our measurements also serve the purpose of studying the contribution of layering to the anisotropy of shales, where the melting kerogen increases the contrast in properties between the layers, thereby increasing the anisotropy. The original kerogen content in a shale also influences the behavior of the shale with temperature. From our study, we see that lean-shales have higher storage moduli and higher Balkulin, A., 2003, Intrinsic and layer-induced vertical transverse isotropy: Geophysics, v. 68/5, p. 1708-1713. Carcione, J.M., 2000, A model for seismic velocity and attenuation in petroleum source rocks: Geophysics, v. 65/4, p. 1080-1092. O'Connell, R.J., and B. Budiansky, 1978, Measures of dissipation in viscoelastic media: Geophysical Research Letters, v. 5/1, p. 5-8. Thomsen, L., 1986, Weak elastic anisotropy: Geophysics, v. 51/10, p. 1954-1966. Zhu, Y., and I. Tsvankin, 2006, Plane-wave propagation in attenuative transversely isotropic media: Geophysics, v. 71/2, p. T17-T30. |