|
Figure
and TableCaptions
 Formation Formation of Hydrate of Hydrate
Let’s consider
how the  formation formation of hydrate causes a high concentration of natural
gases by comparing the physical sizes of a sediment grain size and a
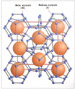
unit-volume of hydrate. A unit-volume of Structure I hydrate is shown as
Figure 1. Limited page space does not permit the unit-volume geometries
of Structure II and Structure H hydrates to be illustrated. This
crystalline structure is called a “unit-volume” because Structure I
hydrate grows in increments of this fundamental building block. This
unit-volume consists of eight cages of structured of hydrate causes a high concentration of natural
gases by comparing the physical sizes of a sediment grain size and a
unit-volume of hydrate. A unit-volume of Structure I hydrate is shown as
Figure 1. Limited page space does not permit the unit-volume geometries
of Structure II and Structure H hydrates to be illustrated. This
crystalline structure is called a “unit-volume” because Structure I
hydrate grows in increments of this fundamental building block. This
unit-volume consists of eight cages of structured  water water that can each
trap one gas molecule. that can each
trap one gas molecule.
Dendy Sloan at
the Colorado School of Mines (e.g., Sloan, 2003, 2004) defines the
diameter of each cage of this unit-volume as a length that varies from 8
to 10 angstroms. Because any arbitrary diameter across this unit-volume
will span no more than six cages (probably no more than four cages,
actually), the diameter of a unit-volume of hydrate is less than 60
angstroms (6 x 10-9 m).
For a size
comparison, sedimentologists define the low end of very fine-grained
sand to be fragments of sediment that have diameters of about 60 microns
(micrometers) (6 x 10-5 m). The diameter of very fine-grained
sand is thus larger than the diameter of a unit-volume of hydrate by a
factor of 104.
Because the
volume of an object is proportional to (diameter)3, if we
ratio the volume of a very fine-grained sand and the volume of a
unit-volume of hydrate, we find that this 104 difference in
diameters means that 1012 unit-volumes of hydrate can fit
into the space occupied by one very fine sand grain. Assuming that on
average only 80 percent of the eight cages in a unit-volume manage to
trap a gas molecule, hydrate  formation formation causes approximately 6 x 1012
gas molecules to be compressed into a volume equal to that of a single
very fine sand grain. causes approximately 6 x 1012
gas molecules to be compressed into a volume equal to that of a single
very fine sand grain.
This
simple arithmetic supports the statement by Pellenbarg and Max (2001)
that hydrate has the highest energy  density density (184,000 BTU/ft3)
of any form of biogenic or thermogenic gas found naturally. By
comparison, liquid natural gas (LNG) represents the highest energy (184,000 BTU/ft3)
of any form of biogenic or thermogenic gas found naturally. By
comparison, liquid natural gas (LNG) represents the highest energy
 density density (430,000 BTU/ft3) of natural gas that humans can
create using cryogenic technology. (430,000 BTU/ft3) of natural gas that humans can
create using cryogenic technology.
Hydrate thus has an energy  density density Egh that is 0.42 that of
the energy Egh that is 0.42 that of
the energy  density density ELNG of LNG. For any deepwater,
near-seafloor sediments where clusters of hydrate unit-volumes can be
assumed to be distributed throughout the sediment pore space, the energy ELNG of LNG. For any deepwater,
near-seafloor sediments where clusters of hydrate unit-volumes can be
assumed to be distributed throughout the sediment pore space, the energy
 density density of the gas trapped in the structured- of the gas trapped in the structured- water water prison cells of this
dispersed hydrate can be expressed as: prison cells of this
dispersed hydrate can be expressed as:
Egh =
(0.42fCgh)ELNG
where
f is the
porosity of the host sediment containing the hydrate.
Table 1 shows
how Egh is related to ELNG for:
1)
Common porosity ranges found in deepwater, near-seafloor
sediment.
2) That range of
Cgh that causes the reaction “Too bad the concentration is so
low.”
Now
let us consider a specific example: If a hydrate system has a porosity
of 0.5 and a hydrate concentration of 0.5, how large does a hydrate
accumulation have to be in order to have an amount of stored energy that
equals the energy stored in one LNG tanker? Simply solve the
energy-balance equation:
Egh(hydrate
reservoir volume) = ELNG(tanker volume)
Using the ratio
Egh/ELNG = 0.1 from Table 1 for
f = 0.5,
and Cgh = 0.5, the result is:
Hydrate
reservoir volume = 10 LNG tanker volumes.
If we assign
length, width and depth dimensions of 600, 100 and 50 feet to our
hypothetical LNG tanker volume, the size of the hydrate reservoir that
has the same equivalent stored energy is 826 acre-ft (~106 m3).
Thus, when the hydrate
concentration in deepwater sediments is only 0.5 of the available pore
space, we see that there is a tremendous amount of gas in a small volume
of sediment.
When Mother
Nature causes hydrate to form, the result is an impressive concentration
of energy that is independent of burial depth. Because structured- water water hydrate has a large bulk modulus and is difficult to compress, hydrate
will have the same crystalline structure, and thus the same energy
hydrate has a large bulk modulus and is difficult to compress, hydrate
will have the same crystalline structure, and thus the same energy
 density density of entrapped gas, whether at the seafloor or buried deeply
beneath. of entrapped gas, whether at the seafloor or buried deeply
beneath.
This concept
about the relationship between gas concentration and confining pressure
differs from the logic that has to be used in dealing with compressible
gases found in conventional reservoirs. Therefore, there may be a large
number of LNG tanker equivalents awaiting the bold who initiate
deepwater hydrate production.
The only intent
of this discussion is to illustrate that a tremendous amount of energy
is stored in deepwater hydrate. What has been avoided is any discussion
of the challenges of trying to produce that hydrate.
As a
geophysicist, I have two observations about strategies for producing
deep- water water hydrate: hydrate:
1) Hydrate
production is the engineer’s problem.
2) I am glad I
am not the engineer assigned to the problem.
For
geophysicists, it is exciting to try to unravel the mysteries of
deepwater hydrate systems using 4C OBC seismic data and rock physics
theory. Refer to Hardage and Murray (2006), if you wish to know how some
of this multi-component seismic research is being done.
References
Hardage, Bob A., and Paul E. Murray, 2006, High
resolution P-P imaging of deepwater near-seafloor geology and High
resolution P-SV imaging of deepwater near-seafloor geology: Search and
Discovery Article #40200 (2006) (http://www.searchanddiscovery.net/documents/2006/06054hardage06/index.htm)
Pellenbarg, Robert
E., and Michael D. Max, 2001,
Gas hydrates: From laboratory
curiosity to potential global powerhouse: Journal of Chemical Education,
v. 78, p. 896-900.
Sloan, E.D., 2003, Fundamental principles and
applications of natural gas hydrates: Nature (invited review), v. 426,
p. 353-359.
Sloan, E.D.,
2004, Introductory overview: hydrate knowledge development," American
Mineralogist, v. 89, p. 1155-1161.
Return to top.
|
 Click to view article in PDF format.
Click to view article in PDF format.
 Density
Density of Deepwater Gas Hydrate*
of Deepwater Gas Hydrate* formation
formation velocity
and resistivity to hydrate concentration (Cgh) in deepwater,
near-seafloor sediments. Our studies indicate that in numerous targeted
intervals across the Gulf of Mexico, Cgh is 0.5 to 0.6 of the
available pore space in unconsolidated deepwater sediments.
velocity
and resistivity to hydrate concentration (Cgh) in deepwater,
near-seafloor sediments. Our studies indicate that in numerous targeted
intervals across the Gulf of Mexico, Cgh is 0.5 to 0.6 of the
available pore space in unconsolidated deepwater sediments.