Abstract/Excerpt

Secondary Migration of Petroleum as a Highly Efficient, Self-Adjusting Process with Little or No Capillary Resistance

John G. Stainforth
Consultant geologist/geochemist, Katy, Texas, USA

The problem of secondary migration of petroleum is as old as the petroleum industry itself, yet still no consensus has been reached on the mechanism(s), contrary to widespread opinion. The situation has been muddied recently by promotion of certain mechanisms simply on grounds of computational expediency. The result is that the subject of secondary migration is now in disarray.

In this paper, I briefly review mechanisms that have been proposed for secondary migration and their shortcomings. Then, I outline a new hypothesis that appears to overcome these difficulties.

From the earliest days, many workers found secondary migration to be a fascinating unsolved problem; a perpetual mystery, with deceptively complex mechanisms of obscure nature that are not well understood. The early workers invoked migration of petroleum in its own separate phase, based on their experience of producing oil and gas fields. This hypothesis immediately presented problems: droplets have inadequate buoyancy to overcome the capillary entry pressure of pore throats, so that they have to coalesce (how? a Catch-22) into long, continuous phase segments that have been called slugs, filaments or stringers. The vertical heights of these have to be in the order of meters to overcome the capillary entry pressures in typical carrier beds. But, the early proponents of this hypothesis were bothered by the lack of observations of:

• Petroleum stringers or slugs of the predicted length (10s of meters) and thickness (meters)
• Petroleum stringers or slugs waiting for take-off on the top of source rocks or at permeability interfaces
• Residual petroleum saturations that should be left in the wake of these slugs, according to capillarity theory
• Differences in the ease or migration for different petroleum types, on account of their widely differing properties (capillary entry pressures and viscosities)

So, the opposite end-member model of migration in solution in static water was studied: it was found to be inadequate, because of the very low solubilities and diffusion rates of petroleum. Thus, flowing water had to be invoked, but compactional and artesian (hydrodynamic) flows are generally too slow to account for the observed volumes of migrated petroleum. Also, the wholesale convection of pore water in carrier beds has been found to be a rare phenomenon that is generally denied by stratified water chemistry.

The next step was to call upon migration of petroleum in water in higher concentrations, in the form of colloids or emulsions, but the problem of this was the large soap-hydrocarbon ratios required for solubilization. Others pointed out that microdroplets could pass through pore-throats without capillary impediment, which was supported by some experiments half a century ago on the migration of oil and gas in the form of fine droplets and bubbles.

Rather suddenly, in the late 1970’s and 1980’s, migration of petroleum as a continuous separate phase became "well-established" (e.g. Berg, 1975; Schowalter, 1979; England et al., 1987), without there actually being significant new data to support the hypothesis. Soon the textbooks were claiming secondary migration to be "well studied and well understood." The basis for this renewed confidence eluded this author.

As we entered the age of computer modeling, the only problem that proponents of this hypothesis seem to have had was its use of Darcy’s law to describe the actual movement of petroleum slugs, simply on the grounds that this is computationally very slow. So, they looked for faster computational approaches, such as invasion percolation models that treat viscous forces as negligible. According to invasion percolation theory, migration is controlled only by the balance between buoyancy and capillary forces.

Losses of petroleum along migration paths are an issue of concern with the separate phase flow and invasion percolation hypotheses, because they predict trails of residual petroleum, trapped by capillarity, along migration pathways. But there is a total lack of consensus on the magnitudes of these residual saturations. Some authors claim that they "are likely to be very large in relation to volumes trapped", whilst others say they are "mostly small"; some say they are "almost impossible to quantify", whilst others claim they "can be calculated to a high degree of accuracy".

Desirable features of a secondary migration mechanism

a) In line with field observations, secondary migration should work similarly for all petroleum types, from highly viscous, heavy oil to dry gas. This is not the case for migration in continuous, separate phases, because viscosities and capillary entry pressures of petroleum vary by many orders of magnitude.

b) Mass continuity should be maintained throughout the migration network, otherwise petroleum would pile up locally along migration routes (and not just in the trap). Ultimately, the flow rates should balance the expulsion fluxes of petroleum out of the source rock. The focusing of migration into anticlines and structural noses shows that flow rates and fluxes probably vary by 6 or 7 orders of magnitude within a single secondary migration system. This suggests that the petroleum flow rates should be capable of self-adjustment over this entire spectrum of rates. Migration in the form of slugs and filaments does not naturally meet this requirement.

c) Nature likes to lose energy as fast as possible, whilst minimizing energy dissipation. The movement of slugs and filaments, in spasmodic fits and starts, seems very unlikely to conform to this principle.

New hypothesis: flow of metastable clusters and microdroplets of petroleum

In view of the problems of migration in either ordinary water solution, or in emulsions, or in continuous separate phase, one finally turns to an area that has not been adequately considered hitherto. This is the metastable region between petroleum in water solution and petroleum in its own separate phase.

Solutes tend to cluster in supersaturated, metastable solutions. This should be particularly true for petroleum in water solution, firstly because petroleum has a hydrophobic tendency to form clusters, and secondly because the interfacial tension between petroleum and water is very high, leading to a very high free energy penalty for forming droplets and bubbles.

Supersaturated solutions generally exist as three species: molecular solute, solvent and solute clusters. Clusters sizes are smaller than the critical nucleus size for droplet formation, i.e., ~ 1000 to 10,000 molecules or ~10 nm, and increase with increasing supersaturation. Eventually, increasing supersaturation causes petroleum to exsolve into microdroplets. It can be shown that these generally meet the required rates of migration, driven by buoyancy, at sizes considerably smaller than those of pore throats in typical carrier beds, and so they are not subject to capillary resistance. The velocities of petroleum clusters and microdroplets of radius r are proportional to r², in accordance with Stoke’s Law.

Implications of the proposed hypothesis

Cluster formation occurs in the metastable region between solubility and exsolution and does not require solubilizers or emulsifiers.

1) There are no capillary constraints. Thus, the ratio of viscous to capillary forces (the Capillary Number) is essentially infinite, unlike in continuous, separate phase flow, where it is typically < 10^-6 and often ignored (as in invasion percolation models). Likewise, the ratio between buoyant and capillary forces (the Bond number) is extremely large, unlike in invasion percolation models in which it is negligibly small.

2) The flux of petroleum in clusters or droplets J_sc, through a rock whose pore throats are just large enough to allow passage of the clusters without capillary restraint, can be compared with separate phase Darcy flux J_do through the same rock. To first approximation, the ratio of these fluxes is proportional to the ratio of the kinematic viscosities of the oil and water:

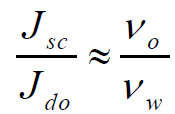
Water is less viscous than even the lowest viscosity oil, so generally v_o > v_w or v_o >> v_w. Thus, the flux of oil in clusters and droplets is generally faster or much faster than the Darcy flux of a continuous, separate phase.

3) The mechanism works for all types of petroleum with similar ease and velocity, because the flow rates are controlled not by the highly variable viscosities of petroleum but by the viscosity of water, which varies mainly with temperature alone.

4) The range of petroleum velocities and fluxes with this hypothesis is very great. The radii r of clusters and microdroplets are less than the diameters of the neighboring pore throats, which in carrier beds vary from ~ 10^-8 to 10^-4 m. Thus, r varies by about four orders of magnitude, and the velocities of the clusters or droplets by about eight orders of magnitude.

5) The mechanism is self-adjusting. If the mass transport by the petroleum clusters or droplets lags behind the petroleum influxes anywhere in the migration network (such as the expulsion fluxes from the source rock), the supersaturation of petroleum in the pore water increases. This causes the clusters to increase in size and speed up (with the square of their size), and v.v. The same holds for microdroplets. The calculated range of velocities is from ~1 cm/yr to ~10 km/yr!

6) The mass flow rates are more or less balanced throughout the migration network, so that petroleum does not accumulate anywhere in the migration system except in trap(s); the mass continuity requirement is satisfied naturally.

7) Petroleum clusters and droplets undergo Brownian motion, which should aid their passage through pore throats and prevent their sticking to walls. Brownian motion decreases with increasing size of the clusters and microdroplets. (For macroscopic droplets and bubbles, Brownian motion would be negligible.)

8) For the slower cluster and microdroplet velocities predicted in the early stages of secondary migration, compactional and artesian flows of pore water are (relatively) quite important. These slow flows of water aid vertical migration of clusters from the source rock up to the first seal, and their subsequent lateral migration beneath the seal.

9) In spite of the all-important role of clusters and microdroplets in this hypothesis, their volume fractions in the pores are relatively small (~0.001 or less).

10) The losses of petroleum into water solution are very small compared with the total quantities of petroleum migrated, so the mechanism is very highly efficient (~100%). Virtually no residual petroleum is left along migration routes.

11) It should be possible to establish fractal stream laws, similar to Horton’s Laws for river networks, to calculate flow rates and fluxes throughout secondary migration networks.

AAPG Search and Discovery Article #120098©2013 AAPG Hedberg Conference Petroleum Systems: Modeling the Past, Planning the Future, Nice, France, October 1-5, 2012