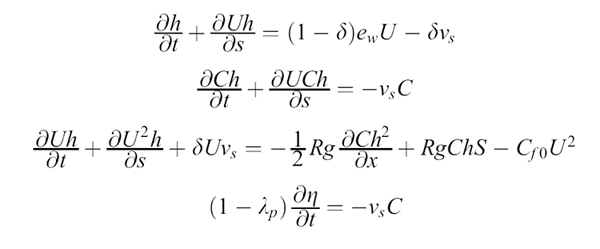![]() Click to view article in PDF format.
Click to view article in PDF format.
Depositional Turbidity Currents in Diapiric Minibasins on the Continental Slope: Theory, Experiments, and Numerical Simulation*
By
Horacio Toniolo1 and Gary Parker2
Search and Discovery Article #40111 (2004)
*Adapted from “extended abstract” for presentation at the AAPG Annual Meeting, Salt Lake City, Utah, May 11-14, 2003.
1University of Alaska Fairbanks, Fairbanks, AK;
2University of Minnesota, Minneapolis, MN
The northern continental slope of the Gulf of Mexico is riddled with numerous subsiding diapiric minibasins bounded by ridges, many of which are connected by channels created by turbidity currents. The region is economically relevant in that these diapiric minibasins constitute focal points for the deposition of sand. These deposits in turn serve as excellent reservoirs for hydrocarbons. A better understanding of the ‘‘fill and spill’’ process by which minibasins fill with sediment as the intervening ridges are dissected by canyons may serve to aid in the location of such reservoirs. A theory is developed to describe sediment deposition in minibasins. Two key and heretofore unrecognized aspects of the ‘‘fill and spill’’ process are revealed:
-
The formation of an internal hydraulic jump as a turbidity current spills into a confined basin.
-
The detrainment of water across a settling interface forming at the top of the ponded turbidity current downstream of the hydraulic jump.
It is shown that sufficiently strong detrainment can consume the flow, so that there is no outflow of either water or sediment even with continuous inflow. As the basin fills with sediment, however, overspill is eventually realized. The theory is developed into a numerical model, tested against laboratory experiments. The result is a view of intraslope minibasin sedimentation that has a stronger physical basis than the conceptual models proposed to date.
|
|
Turbidity currents on the continental slope have created a rich morphodynamic and stratigraphic history associated with erosion and deposition. The continental slope of the northern Gulf of Mexico offers a unique opportunity to study both of these simultaneously. The most distinctive aspect of deep-water sedimentation in that region is the influence of numerous subsiding salt-withdrawal minibasins that have trapped thick sedimentary sections containing sand bodies with excellent hydrocarbon reservoir properties. These basins are shown in Figure 1 (Pratson and Haxby, 1997). Each basin is bounded by ridges that have been uplifted as a compensatory effect of basin subsidence. Many but not all of these minibasins are interconnected by drainage networks of turbidity current channels (e.g., Liu and Bryant, 2000). The turbidity currents that created these channels have cut through the ridges to create canyons, and deposited sediment in the minibasins themselves, a process that has been documented by Beaubouef and Friedman (2000), for example. As noted above, minibasins often contain sand bodies that serve as good hydrocarbon reservoirs. In order for a turbidity current to deposit within a minibasin, however, it first must reach the minibasin. The initial stages by which this occurs can be envisioned in terms of a turbidity current that runs down the relatively steep slope of the updip rim of the minibasin, ponds within it, deposits sediment and eventually overflows. This process has been familiarly termed ‘‘fill and spill’’ (e.g., Winker, 1996). One approach to the study of the process of ‘‘fill and spill’’ is the analysis of the modern seafloor and the first few hundred meters below that level, using acoustic images of bathymetry and high-resolution seismic surveys and borehole drilling programs (e.g., Damuth et al., 1983; Winker, 1996; Liu and Bryant, 2000; Pirmez et al., 2000, among many others). Such analyses have served to clarify many aspects of minibasins and the process by which they fill, several of which have been incorporated into the present work. In particular, they have revealed that the ultimate effect of ‘‘fill and spill’’ is to create a channel that cuts deeply though successive ridges and fills in successive basins, thereby connecting the basins and creating a channel with a relatively constant slope throughout (Beaubouef and Friedman, 2000). These studies have, however, led to debate concerning the precise mechanism of ‘‘fill and spill.’’ At one end is the possibility that very large, sustained turbidity currents cascade from one basin to the next, simultaneously sculpting the channel during each event. At the other end is the possibility that small, pulse-like events must substantially fill each minibasin before enough overflow occurs to initiate erosion through the ridge at the downdip end and start the process of filling of the next basin. Theory, experiment, and numerical modeling offer alternate avenues to gain further insight in the process of ‘‘fill and spill.’’ These avenues are explored here. They reveal a third, heretofore unrecognized possibility for the mechanism of ‘‘fill and spill:’’ namely, that sustained turbidity currents capable of eroding through the ridges may nevertheless be incapable of flowing out of a minibasin until the relief of the minibasin has been substantially reduced. Put in its simplest terms, the analysis presented here indicates that a turbidity current flowing continuously into a minibasin may produce no outflow whatsoever.
This work focuses on the study of minibasin deposition in a highly simplified configuration. A slot-like minibasin is assumed to be much longer than it is wide. The turbidity current flowing into it is continuous and carries a dilute suspension of sediment of uniform size. The minibasin is assumed to have sufficient relief to cause the inflowing turbidity current to undergo a hydraulic jump, so creating a muddy pond containing a dilute suspension of very slowly moving water and sediment. The interface between the muddy pond and the clear water above defines a settling interface. This interface may be above the elevation of the lip at the downstream end of the pond, in which case the turbid water overflows the basin, or below it, in which case there is no overflow. In the latter case all the sediment is lost to bed deposition and all the inflowing water is lost to detrainment across the settling interface. This geometry is illustrated in Figure 2. The above simplifications serve to clearly define the roles of the internal hydraulic jump and water detrainment in mediating the process of minibasin deposition. As mentioned before, if the relief of the basin is sufficient, a turbidity current emanating down from a ridge is forced to undergo a hydraulic jump from a Froude-supercritical flow regime to a highly Froude-subcritical regime, as shown in Figure 2, where Frd denotes the bulk densimetric Froude number of the flow. The result is a zone of ponded turbid water with a very low flow velocity and passive settling out from the turbidity current. The top of the turbid water forms a distinct settling interface, across which water is constantly detrained upward from turbid water to clear water. The capacity for detrainment across the settling interface is huge. Consider, for example, a turbidity current composed of 100 Dm material flowing into a mini-basin with a top area of 10 km2. The detrainment discharge is given as the product of the fall velocity of the sediment times the area of the basin, or in this case 748,000 m3/s. For reference, the highest discharge ever measured on the Amazon River is reported to be 338,000 m3/s. The implication is that a turbidity current with a flow discharge smaller than the detrainment discharge should not escape the basin, even with continuous inflow, until the basin is nearly full with sediment. The model is presented in Toniolo et al. (submitted (a)). It is based on the layer-integrated formulation of Parker et al. (1986) but is modified to capture the effect of water detrainment across the interface between muddy water and clear water above. It solves a set of layer-integrated equations of flow continuity, sediment conservation, and momentum, along with the Exner equation of bed sediment conservation. The equations take the forms:
Where t denotes time s denotes a bed-attached stream-wise coordinate U denotes depth-averaged flow velocity h denotes the layer thickness of the turbidity current d denotes a parameter that is zero in the supercritical region (Frd>1) and 1 in the ponded zone (Frd<<1) ew denotes an entrainment function given by Parker et al. (1986) vs denotes sediment fall velocity C denotes the concentration R denotes the submerged specific gravity S denotes bed slope Cfo denotes the friction coefficient g denotes gravitational acceleration lp denotes porosity of the sediment deposit h denotes the bed elevation from an arbitrary level.
The results of two experiments (Experiments 1 and 3) carried out at St. Anthony Falls Laboratory, University of Minnesota are reported here as a partial test of the above theory. The purpose of the experiments was to provide data for the evaluation of the numerical model of depositional turbidity currents in intra-slope minibasins. This experimental test serves as a useful bridge between the theory and its application to field settings. A basin of simplified geometry was used in the experiments. Its length was 4 m, and the maximum relief was 0.46 m. The geometry was defined by an upstream region of a constant slope S b1 = 0.298 (slope angle qb1 = 16.6o), a nearly horizontal central region with slope S b2 = 0.017 (qb2 = 0.97) and a nearly vertical wall at the downstream end (e.g., Toniolo et al. submitted (b)). The experimental configuration differs from those of natural diapiric minibasins in several ways. Firstly, the uniform width of the experimental configuration yields a slot-like 2D configuration. Most natural minibasins have more rounded 3D configurations, although some slot-like minibasins can be found in the field. Secondly, natural minibasins are not delineated by vertical walls at their downslope ends, but instead show a gradual increase in bed elevation toward a ridge. Glass beads (ballotini) at a volume concentration of 5% were used in both Experiments 1 and 3. The beads were chosen so as to be as nearly uniform in size as possible. The geometric mean size Dg was 46 mm and the geometric standard deviation sg was 1.25. The flow discharges were 0.33 l/s and 1.9 l/s in Experiments 1 and 3, respectively. The low discharge of Experiment 1 was selected specifically to model a turbidity current that would be completely captured in the minibasin despite continuous inflow. The substantially higher discharge of Experiment 3 was selected to model a turbidity current of sufficient strength to continuously overflow the minibasin. The interface at the downstream end of the basin during Experiments 1 and 3 are shown in Figure 3.
Equations 1 - 4 are in conservative form and as such are intrinsically shock-capturing. In the context of the present work, this means that when implemented numerically, the positions of any hydraulic jumps are automatically captured. The MacCormack scheme is used to solve the governing equations. This explicit scheme is second-order accurate both in space and time. The results of the numerical simulation of both experiments are shown in Figure 4. The agreement between experiment and numerical model is very good.
The physically-based theory of sedimentation in minibasins identifies a heretofore poorly-recognized flow regime; i.e., a ponded turbidity current. The ponding is created by an elevation barrier. It forces a relatively swift, Froude-supercritical turbidity current to pass through a type of shock known as an internal hydraulic jump, which results in a deep, placid, slow-moving turbidity current farther downstream. This ponded current may:
In the case of uniform sediment, this results in:
The loss of both sediment and water from the current due to settling and detrainment can weaken it to the point that no overflow whatever occurs, even with continuous inflow. The theory has been implemented numerically and checked against experiments for a slot-like minibasin and a turbidity current with a single grain size. Several predictions of the theory have been verified, including the nearly uniform thickness of the deposit in the ponded zone and the existence of conditions for which overflow of neither water nor sediment occurs at the downstream lip of the basin.
Beaubouef, R.T., and Friedman, S.J., 2000, High resolution seismic/sequence stratigraphic framework for the evolution of Pleistocene intra slope basins, western Gulf of Mexico: depositional models and reservoir analogs: GCSSEPM Foundation 20th Annual Research Conference, Deep-Water Reservoirs of the World, Dec. 3-6, p. 40-60. Damuth, J.E., Kolla, V., Flood, R.D., Kowsmann, R.O., Moonteiro, M.C., Gorini, M.A., Palma, J.J.C., and Belderson, R.H., 1983, Distributary channel meandering and bifurcation patterns on Amazon deep-sea fan as revealed by long-range sidescan sonar (GLORIA): Geology, v. 11, p. 94-98. Liu, J.Y., and Bryant, W.R., 2000, Sea floor morphology and sediment paths of the northern Gulf of Mexico deepwater, in Fine-Grained Turbidite Systems, A.H. Bouma, and C.G. Stone, eds.: AAPG Memoir 72, SEPM Special Publication 68, p. 33-45. Parker, G., Fukushima, Y., and Pantin, H.M., 1986, Self-accelerating turbidity currents: Journal of Fluid Mechanics, v. 171, p. 145-181. Pirmez, C., Beaubouef, R.T., Friedmann, S.J., and Mohrig, D.C., 2000, Equilibrium profile and baselevel in submarine channels: Examples from late Pleistocene systems and implications for the architecture of deepwater reservoirs: GCSSEPM Foundation 20th Annual Research Conference, Deep-Water Reservoirs of the World, Dec. 3-6, p. 782-805. Pratson, L. F., and Haxby, W.F, 1997, Panoramas of the seafloor: Scientific American, no..4, p. 82-87. Toniolo, H., Lamb, M., and Parker, G., submitted (a), Depositional turbidity currents in diapiric minibasins on the continental slope: formulation and theory: Journal of Sedimentary Research. Toniolo, H., Parker, G., and Voller, V., submitted (b), Depositional turbidity currents in diapiric minibasins on the continental slope: experiments and numerical simulation: Journal of Sedimentary Research. Winker, C.D., 1996, High-resolution seismic stratigraphy of a late Pleistocene submarine fan ponded by salt-withdrawal mini-basins on the Gulf of Mexico continental slope: Proceedings of the 28th annual Offshore Technology Conference, p. 619- 628. |